题目内容
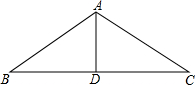已知△ABC中，AB=17cm，BC=30cm，BC上的中线AD=8cm，请你判断△ABC的形状，并说明理由．考点：勾股定理的逆定理,等腰三角形的判定
专题：
分析：首先根据出AD2+BD2=AB2结合勾股定理逆定理可判断△ABD是直角三角形，进而得到AD是BC的垂直平分线，然后根据垂直平分线的性质可得AB=AC．
解答：解：∵BC=30cm，
∴BD=15cm，
∵AD=8cm，AB=17cm，
∴AD2+BD2=AB2，
∴△ABD是直角三角形，
∴AD是BC的垂直平分线，
∴AB=AC，
∴△ABC是等腰三角形．
∴BD=15cm，
∵AD=8cm，AB=17cm，
∴AD2+BD2=AB2，
∴△ABD是直角三角形，
∴AD是BC的垂直平分线，
∴AB=AC，
∴△ABC是等腰三角形．
点评：此题主要考查了勾股定理逆定理，关键是掌握勾股定理的逆定理：如果三角形的三边长a，b，c满足a2+b2=c2，那么这个三角形就是直角三角形．
练习册系列答案
口算题天天练系列答案
相关题目
如图，在矩形ABCD中，对角线BD的垂直平分线MN与AD相交于点M，与BD相交于点O，与BC相交于N，连接MN，DN．当x＞0，y＞0时，下列正确的是（ ）
A、
| ||||
B、
| ||||
C、
| ||||
D、
|
如图，由下列实验可得（ ）
| A、方程两边都加上或都减去同一个数或同一个整式，方程的解不变 |
| B、方程两边都乘以或都除以同一个不为零的数，方程的解不变 |
| C、不等式的两边都加上（或减去）同一个数或同一个整式，不等式的方向不变 |
| D、不等式的两边都乘以（或除以）同一个不为零的数，不等号的方向改变 |
