题目内容
19.如图①,已知∠MON=Rt∠,点A,P分别是射线OM,ON上两定点,且OA=2,OP=6,动点B从点O向点P运动,以AB为斜边向右侧作等腰直角△ABC,设线段OB的长x,点C到射线ON的距离为y.(1)若OB=2,直接写出点C到射线ON的距离;
(2)求y关于x的函数表达式,并在图②中画出函数图象;
(3)当动点B从点O运动到点P,求点C运动经过的路径长.

分析 (1)OB=2时,四边形OACB是正方形,由此即可解决问题.
(2)如图③中,作CE⊥OA于E,CF⊥ON于F.由△CEA≌△CFB,推出AE=CF,CE=CF,由∠CEO=∠CFO=∠EOF=90°,推出四边形OECF是矩形,由CE=CF,
推出四边形OECF是正方形,根据AE=y-2,FB=x-y,可得y-2=x-y,即y=$\frac{1}{2}$x+1(0≤x≤6),画出图象即可.
(3)如图③中,由CE=CF,推出OC平分∠MON,推出点C的运动轨迹是线段OC,因为x=6,y=4,可得OC=4$\sqrt{2}$.
解答 解:(1)如图①中,
∵OA=OB=2,∠AOB=90°,△ACB是等腰直角三角形,
∴四边形OACB是正方形,
∴点C到ON的距离为2.
(2)如图③中,作CE⊥OA于E,CF⊥ON于F.
∵∠ACB=∠ECF=90°,CA=CB,∠CEA=∠CFB=90°,
∴△CEA≌△CFB,
∴AE=CF,CE=CF,
∵∠CEO=∠CFO=∠EOF=90°,
∴四边形OECF是矩形,∵CE=CF,
∴四边形OECF是正方形,
∴CF=CE=OE=OF=y,
∵AE=y-2,FB=x-y,
∴y-2=x-y,
∴y=$\frac{1}{2}$x+1,可得函数图象如图②所示,
(3)如图③中,∵CE=CF,
∴OC平分∠MON,
∴点C的运动轨迹是线段OC,
∵x=6,y=4,
∴OC=4$\sqrt{2}$,
∴点C运动经过的路径长为4$\sqrt{2}$.
点评 本题考查动点问题函数图象、一次函数的应用,全等三角形的判定和性质,解题的关键是学会添加常用辅助线,构造全等三角形解决问题,属于中考常考题型.

练习册系列答案
相关题目
14.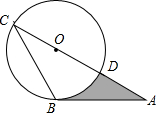 如图,AB是⊙O的切线,B为切点,AC经过点O,与⊙O分别相交于点D、C.若∠CAB=30°,CD=2,则阴影部分面积是( )
如图,AB是⊙O的切线,B为切点,AC经过点O,与⊙O分别相交于点D、C.若∠CAB=30°,CD=2,则阴影部分面积是( )
 如图,AB是⊙O的切线,B为切点,AC经过点O,与⊙O分别相交于点D、C.若∠CAB=30°,CD=2,则阴影部分面积是( )
如图,AB是⊙O的切线,B为切点,AC经过点O,与⊙O分别相交于点D、C.若∠CAB=30°,CD=2,则阴影部分面积是( )| A. | $\frac{\sqrt{3}}{2}$ | B. | $\frac{π}{6}$ | C. | $\frac{\sqrt{3}}{2}$-$\frac{π}{6}$ | D. | $\frac{\sqrt{3}}{3}$-$\frac{π}{6}$ |
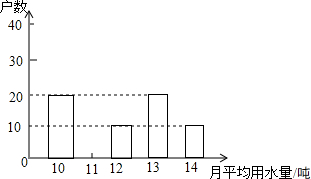 为了倡导“节约用水,从我做起”,某市政府决定对市直机关600户家庭的用水情况作一次调查,市政府调查小组随机抽查了其中的100户家庭一年的月平均用水量 (单位:吨),并将调查结果制成了如图所示的条形统计图.
为了倡导“节约用水,从我做起”,某市政府决定对市直机关600户家庭的用水情况作一次调查,市政府调查小组随机抽查了其中的100户家庭一年的月平均用水量 (单位:吨),并将调查结果制成了如图所示的条形统计图. 如图,矩形OABC在平面直角坐标系xoy中,点A在x轴的正半轴上,点C在y轴的正半轴上,OA=4,OC=3,若抛物线的顶点在BC边上,且抛物线经过O、A两点,直线AC交抛物线于点D(1,n).
如图,矩形OABC在平面直角坐标系xoy中,点A在x轴的正半轴上,点C在y轴的正半轴上,OA=4,OC=3,若抛物线的顶点在BC边上,且抛物线经过O、A两点,直线AC交抛物线于点D(1,n).
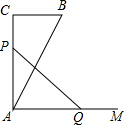 如图,有一Rt△ABC,∠C=90°,AC=10cm,BC=5cm,一条线段PQ=AB,P点在AC上,Q点在过A点且垂直于AC的射线AM上运动.当△ABC和△APQ全等时,点Q到点A的距离为10cm或5cm.
如图,有一Rt△ABC,∠C=90°,AC=10cm,BC=5cm,一条线段PQ=AB,P点在AC上,Q点在过A点且垂直于AC的射线AM上运动.当△ABC和△APQ全等时,点Q到点A的距离为10cm或5cm.