题目内容
14.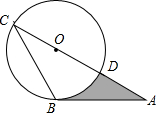 如图,AB是⊙O的切线,B为切点,AC经过点O,与⊙O分别相交于点D、C.若∠CAB=30°,CD=2,则阴影部分面积是( )
如图,AB是⊙O的切线,B为切点,AC经过点O,与⊙O分别相交于点D、C.若∠CAB=30°,CD=2,则阴影部分面积是( )| A. | $\frac{\sqrt{3}}{2}$ | B. | $\frac{π}{6}$ | C. | $\frac{\sqrt{3}}{2}$-$\frac{π}{6}$ | D. | $\frac{\sqrt{3}}{3}$-$\frac{π}{6}$ |
分析 直接利用切线的性质结合扇形面积求法得出阴影部分面积=S△OBA-S扇形OBD,进而得出答案.
解答  解:连接BO,
解:连接BO,
∵AB是⊙O的切线,B为切点,
∴∠OBA=90°,
∵∠CAB=30°,CD=2,
∴OB=1,AO=2,∠BOA=60°,则AB=$\sqrt{3}$,
∴阴影部分面积=S△OBA-S扇形OBD=$\frac{1}{2}$×1×$\sqrt{3}$-$\frac{60π×{1}^{2}}{360}$=$\frac{\sqrt{3}}{2}$-$\frac{π}{6}$.
故选:C.
点评 此题主要考查了切线的性质以及直角三角形的性质,正确得出阴影部分面积=S△OBA-S扇形OBD是解题关键.

练习册系列答案
相关题目


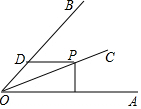 如图,OC平分∠AOB=60°,且∠AOB=60°,点P为OC上任意点,PM⊥OA于M,PD∥OA,交OB于D,若OM=6,则PD的长为( )
如图,OC平分∠AOB=60°,且∠AOB=60°,点P为OC上任意点,PM⊥OA于M,PD∥OA,交OB于D,若OM=6,则PD的长为( )
 在△ABC中,∠C=90°,BC=4cm,∠BAC的平分线交BC于D,且BD:DC=5:3,则D到AB的距离为1.5 cm.
在△ABC中,∠C=90°,BC=4cm,∠BAC的平分线交BC于D,且BD:DC=5:3,则D到AB的距离为1.5 cm.