题目内容
13.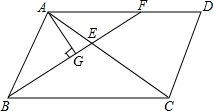 如图,在平行四边形ABCD中,AB=3,BC=5,点F是AD上的一点,且DF=2,连接BF交AC于点E.
如图,在平行四边形ABCD中,AB=3,BC=5,点F是AD上的一点,且DF=2,连接BF交AC于点E.(1)证明:BF平分∠ABC;
(2)过A作AG⊥BF于点G,求$\frac{EG}{EF}$的值.
分析 (1)由平行四边形的性质得出AD=BC=5,AD∥BC,由平行线的性质得出∠AFB=∠CBF,证出AF=AB,由等腰三角形的性质得出∠ABF=∠AFB,证出∠CBF=∠AFB即可;
(2)由平行线得出△AEF∽△CEB,得出对应边成比例$\frac{EF}{BE}=\frac{AF}{BC}$=$\frac{3}{5}$,由等腰三角形的三线合一性质得出BG=FG,即可得出结果.
解答 (1)证明:∵四边形ABCD是平行四边形,
∴AD=BC=5,AD∥BC,
∴∠AFB=∠CBF,AF=AD-DF=5-2=3,
∵AB=3,
∴AF=AB,
∴∠ABF=∠AFB,
∴∠CBF=∠AFB,
∴BF平分∠ABC;
(2)解:∵AD∥BC,
∴△AEF∽△CEB,
∴$\frac{EF}{BE}=\frac{AF}{BC}$=$\frac{3}{5}$,
∵AB=AF,AG⊥BF,
∴BG=FG,
∴$\frac{EG}{EF}$=$\frac{1}{3}$.
点评 本题考查了相似三角形的判定由V型在、平行四边形的性质、比例的性质、等腰三角形的判定与性质;熟练掌握平行四边形的性质,证明三角形相似是解决问题的关键.

练习册系列答案
 53随堂测系列答案
53随堂测系列答案
相关题目
1.下列各组条件中,能判断两个直角三角形全等的是( )
| A. | 一组边对应相等 | B. | 两组直角边对应相等 | ||
| C. | 两组锐角对应相等 | D. | 一组锐角对应相等 |
3.已知点O为△ABC的外心,若∠A=40°,则∠BOC的度数为( )
| A. | 40° | B. | 60° | C. | 80° | D. | 100° |
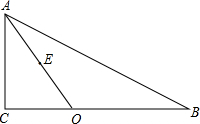 如图,在Rt△ABC中,∠C=90°,AC=4,O是BC上一点,且OC=3,E是AO的中点,如以O为圆心,OC为半径作圆,求点E和⊙O的位置关系.
如图,在Rt△ABC中,∠C=90°,AC=4,O是BC上一点,且OC=3,E是AO的中点,如以O为圆心,OC为半径作圆,求点E和⊙O的位置关系.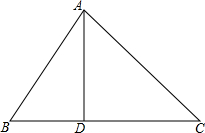 如图,D是△ABC中BC边上一点,∠B=∠DAC,AB2=BD•BC.求证:△ABD∽△CAD.
如图,D是△ABC中BC边上一点,∠B=∠DAC,AB2=BD•BC.求证:△ABD∽△CAD.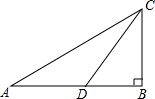 如图,Rt△ABC中,∠ABC=90°,点D在直角边AB上,且∠DCB=∠A.
如图,Rt△ABC中,∠ABC=90°,点D在直角边AB上,且∠DCB=∠A. 如图,已知:AB⊥BC,DC⊥BC,AB=4,CD=2,BC=8,P是BC上的一个动点,设BP=x.
如图,已知:AB⊥BC,DC⊥BC,AB=4,CD=2,BC=8,P是BC上的一个动点,设BP=x.