题目内容
16.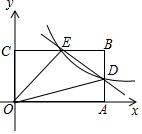 如图,在平面直角坐标系中,矩形OABC的顶点A、C分别在x轴和y轴上,点B的坐标为(6,4),双曲线y=$\frac{k}{x}$(x>0)经过AB的中点D,且与BC交于点E,连接DE.
如图,在平面直角坐标系中,矩形OABC的顶点A、C分别在x轴和y轴上,点B的坐标为(6,4),双曲线y=$\frac{k}{x}$(x>0)经过AB的中点D,且与BC交于点E,连接DE.(1)求k的值和直线DE的解析式;
(3)若点P是y轴上一点,且△OPE的面积与四边形ODBE的面积相等,求点P的坐标.
分析 (1)根据AB的中点D(6,2)求得双曲线解析式,继而结合矩形的性质知点E(3,4),待定系数法求得直线DE的解析式;
(2)先利用割补法求得四边形的面积,再依据△OPE的面积与四边形ODBE的面积相等求得点P的纵坐标即可得出答案.
解答 解:(1)∵点B的坐标为(6,4),
∴AB的中点D的坐标为(6,2),
将点D(6,2)的坐标代入y=$\frac{k}{x}$(x>0),
得:k=6×2=12.
∵BC∥x轴,
∴点E的纵坐标与点B的纵坐标相等,
∴点E的纵坐标为4.
∵点E在双曲线上,
∴x=$\frac{12}{4}$=3,
∴点E在坐标为(3,4).
设直线DE的解析式为y=kx+b(k≠0),
将点D(6,2)、E(3,4)的坐标代入,
得:$\left\{\begin{array}{l}{3k+b=4}\\{6k+b=2}\end{array}\right.$,
解得:$\left\{\begin{array}{l}{k=-\frac{2}{3}}\\{b=6}\end{array}\right.$.
∴直线DE的解析式为y=-$\frac{2}{3}$x+6.
(2)∵S四边形ODBE=S矩形OABC-S△OAD-S△OCE=6×4-$\frac{1}{2}$×6×2-$\frac{1}{2}$×4×3=12,
∴$\frac{1}{2}$×OP×CE=12,即$\frac{1}{2}$×OP×3=12,
∴OP=8.
∴点P的坐标为(0,8)或(0,-8).
点评 本题主要考查直线和双曲线的交点问题,熟练掌握待定系数法求函数解析式及割补法求四边形的面积、矩形的性质是解题的关键.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
7.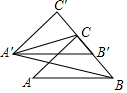 把△ABC沿BC方向平移,得到△A′B′C′,随着平移距离的不断增大,△A′CB的面积大小变化情况是( )
把△ABC沿BC方向平移,得到△A′B′C′,随着平移距离的不断增大,△A′CB的面积大小变化情况是( )
 把△ABC沿BC方向平移,得到△A′B′C′,随着平移距离的不断增大,△A′CB的面积大小变化情况是( )
把△ABC沿BC方向平移,得到△A′B′C′,随着平移距离的不断增大,△A′CB的面积大小变化情况是( )| A. | 增大 | B. | 减小 | C. | 不变 | D. | 不确定 |
4.某新建火车站站前有一块长为20米,宽为8米的矩形空地,计划在其中修建两块相同的矩形绿地,它们的面积之和为56米2,两块绿地之间及周边留有宽度相等的人行通道(如图所示),则人行通道的宽度是( )


| A. | 1 米 | B. | 2米 | C. | $\frac{26}{3}$米 | D. | 2米或$\frac{26}{3}$米 |
5.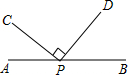 如图,点P在直线AB上,点C,D在直线AB的上方,且PC⊥PD,∠APC=28°,则∠BPD的度数为( )
如图,点P在直线AB上,点C,D在直线AB的上方,且PC⊥PD,∠APC=28°,则∠BPD的度数为( )
 如图,点P在直线AB上,点C,D在直线AB的上方,且PC⊥PD,∠APC=28°,则∠BPD的度数为( )
如图,点P在直线AB上,点C,D在直线AB的上方,且PC⊥PD,∠APC=28°,则∠BPD的度数为( )| A. | 28° | B. | 60° | C. | 62° | D. | 152° |
 如图所示,图中是某中学初一(1)班某次期中考试成绩各个分数段人数的统计图,已知其中不及格同学的人数占全班人数的$\frac{1}{13}$.
如图所示,图中是某中学初一(1)班某次期中考试成绩各个分数段人数的统计图,已知其中不及格同学的人数占全班人数的$\frac{1}{13}$.