题目内容
5.阅读下面问题:$\frac{1}{\sqrt{2}+1}=\frac{1×(\sqrt{2}-1)}{(\sqrt{2}+1)(\sqrt{2}-1)}$=$\sqrt{2}-1$$\frac{1}{\sqrt{3}+\sqrt{2}}=\frac{\sqrt{3}-\sqrt{2}}{(\sqrt{3}+\sqrt{2})(\sqrt{3}-\sqrt{2})}$=$\sqrt{3}-\sqrt{2}$
$\frac{1}{\sqrt{4}+\sqrt{3}}=\frac{\sqrt{4}-\sqrt{3}}{(\sqrt{4}+\sqrt{3})(\sqrt{4}-\sqrt{3})}$=$\sqrt{4}-\sqrt{3}$
…
(1)通过以上计算,观察规律,写出第n个式子$\sqrt{n+1}$-$\sqrt{n}$.
(2)试求$\frac{1}{1+\sqrt{2}}+\frac{1}{\sqrt{2}+\sqrt{3}}+…+\frac{1}{\sqrt{99}+\sqrt{100}}$的值.
分析 (1)根据平方差公式分母有理化,归纳规律;
(2)根据(1)中的规律进行分母有理化,运算即可.
解答 解:(1)$\frac{1}{\sqrt{n+1}+\sqrt{n}}$=$\sqrt{n+1}$-$\sqrt{n}$,
故答案为:$\sqrt{n+1}$-$\sqrt{n}$;
(2)原式=$\sqrt{2}-1$+$\sqrt{3}-\sqrt{2}$+…$\sqrt{100}$-$\sqrt{99}$
=$-1+\sqrt{100}$
=-1+10
=9.
点评 本题主要考查了运用平方差公式进行分母用理化,理解分母有理化,发现(1)中的规律是解决此题的关键.

练习册系列答案
相关题目
15.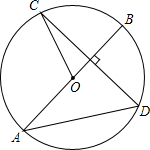 如图,线段AB是圆O的直径,弦CD⊥AB,如果∠BOC=70°,那么∠BAD等于( )
如图,线段AB是圆O的直径,弦CD⊥AB,如果∠BOC=70°,那么∠BAD等于( )
 如图,线段AB是圆O的直径,弦CD⊥AB,如果∠BOC=70°,那么∠BAD等于( )
如图,线段AB是圆O的直径,弦CD⊥AB,如果∠BOC=70°,那么∠BAD等于( )| A. | 20° | B. | 30° | C. | 35° | D. | 70° |
13.某景点的门票价格如下表:
某校八年级(一)、(二)两班共102人去游览该景点,其中(一)班不足50人,(二)班多于50人但不足60人,如果两班都以班为单位分别购票,则一共付款1118元.
(1)两班各有多少名学生?
(2)如果你是购票决策人,将如何购票能够省钱?可节省多少钱?
| 购票人数 | 1~50人 | 51~100人 | 100人以上 |
| 每人门票价 | 12元 | 10元 | 8元 |
(1)两班各有多少名学生?
(2)如果你是购票决策人,将如何购票能够省钱?可节省多少钱?
20.下列结论正确的是( )
| A. | 对角线相等的四边形是矩形 | |
| B. | 对角线互相平分的四边形是矩形 | |
| C. | 对角线互相垂直且平分的四边形是矩形 | |
| D. | 对角线互相平分且相等的四边形是矩形 |
10.将点A(-3,-2)向左平移5个单位,再向下平移4个单位得到点B,则点B的坐标为( )
| A. | (-8,2) | B. | (-8,-6) | C. | (2,-2) | D. | (2,2) |
17.如果单项式2xm+2ny与-3x4y4m-2n是同类项,则m、n的值为( )
| A. | m=-1,n=2.5 | B. | m=1,n=1.5 | C. | m=2,n=1 | D. | m=-2,n=-1 |
 (1)已知关于x的一元二次方程x2-4x+m-1=0有两个相等的实数根,求m的值及方程的根.
(1)已知关于x的一元二次方程x2-4x+m-1=0有两个相等的实数根,求m的值及方程的根.