题目内容
16. (1)已知关于x的一元二次方程x2-4x+m-1=0有两个相等的实数根,求m的值及方程的根.
(1)已知关于x的一元二次方程x2-4x+m-1=0有两个相等的实数根,求m的值及方程的根.(2)如图,已知?ABCD,E、F是对角线BD上的两点,且BE=DF
①求证:四边形AECF是平行四边形;
②当AE垂直平分BC且四边形AECF为菱形时,直接写出AE:AB的值.
分析 (1)首先根据原方程根的情况,利用根的判别式求出m的值,即可确定原一元二次方程,进而可求出方程的根,
(2)①连接AC交BD于点O,根据平行四边形的对角线互相平分可得OA=OC,OB=OD,然后求出OE=OF,再根据对角线互相平分的四边形是平行四边形即可证明;
②根据菱形的对角线互相垂直可得AC⊥EF,从而得到AC⊥BD,所以?ABCD需要满足是菱形,即邻边相等,然后由锐角三角函数求得.
解答 解:(1)由题意可知△=0,即(-4)2-4(m-1)=0,解得m=5.
当m=5时,原方程化为x2-4x+4=0.解得x1=x2=2.
所以原方程的根为x1=x2=2; (2)①证明:如图,连接AC交BD于点O,
(2)①证明:如图,连接AC交BD于点O,
在?ABCD中,OA=OC,OB=OD,
∵BE=DF,
∴OB-BE=OD-DF,
即OE=OF,
∴四边形AECF是平行四边形;
②当AE垂直平分BC且四边形AECF为菱形时,
AC垂直平分EF,
∴?ABCD是菱形,
∴AB=BC,
设AE交BC于H,
∴AH=$\frac{\sqrt{3}}{2}$AB,EH=$\frac{\sqrt{3}}{6}$AB,
∴AE=AH-EH=$\frac{\sqrt{3}}{3}$AB,
∴AE:AB=$\frac{\sqrt{3}}{3}$.
点评 本题考查了一元二次方程根的情况与判别式△的关系:菱形的判定,平行四边形的判定,主要利用了对角线互相平分的四边形是平行四边形,邻边相等的平行四边形是菱形,作出辅助线是解题的关键.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
6.下列二次根式中,最简二次根式是( )
| A. | $\sqrt{8}$ | B. | $\sqrt{169}$ | C. | $\sqrt{{x^2}+4}$ | D. | $\sqrt{\frac{1}{x}}$ |
7. 如图,已知直线a,b被直线c所截,那么∠1的同位角是( )
如图,已知直线a,b被直线c所截,那么∠1的同位角是( )
 如图,已知直线a,b被直线c所截,那么∠1的同位角是( )
如图,已知直线a,b被直线c所截,那么∠1的同位角是( )| A. | ∠5 | B. | ∠4 | C. | ∠3 | D. | ∠2 |
4.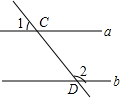 如图,直线a∥b,直线DC与直线a相交于点C,与直线b相交于点D,已知∠1=25°,则∠2的度数为( )
如图,直线a∥b,直线DC与直线a相交于点C,与直线b相交于点D,已知∠1=25°,则∠2的度数为( )
 如图,直线a∥b,直线DC与直线a相交于点C,与直线b相交于点D,已知∠1=25°,则∠2的度数为( )
如图,直线a∥b,直线DC与直线a相交于点C,与直线b相交于点D,已知∠1=25°,则∠2的度数为( )| A. | 135° | B. | 145° | C. | 155° | D. | 165° |
6.下列计算中,正确的是( )
| A. | a2+b3=2a5 | B. | (-a3b)2=a6b2 | C. | a2•a3=a6 | D. | a4÷a=a4 |
 如果按图中虚线对折可以做成一个上底面为无盖的盒子,那么该盒子的下底面的字母是B.
如果按图中虚线对折可以做成一个上底面为无盖的盒子,那么该盒子的下底面的字母是B.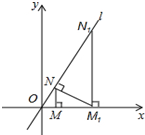 如图,已知直线l:y=$\sqrt{3}x$(直线l与x轴的夹角是60°),过点M(2,0)作x轴的垂线交直线l于点N,过点N作直线l的垂线交x轴于点M1;过点M1作x轴的垂线交直线l于N1,过点N1作直线l的垂线交x轴于点M2,…;按此作法继续下去,则点Mn的坐标为(22n+1,0).
如图,已知直线l:y=$\sqrt{3}x$(直线l与x轴的夹角是60°),过点M(2,0)作x轴的垂线交直线l于点N,过点N作直线l的垂线交x轴于点M1;过点M1作x轴的垂线交直线l于N1,过点N1作直线l的垂线交x轴于点M2,…;按此作法继续下去,则点Mn的坐标为(22n+1,0).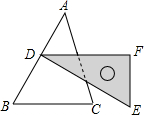 如图,含30°角的直角三角尺DEF放置在△ABC上,30°角的顶点D在边AB上,DE⊥AB,若∠B为锐角,BC∥DF,则∠B的大小为60°.
如图,含30°角的直角三角尺DEF放置在△ABC上,30°角的顶点D在边AB上,DE⊥AB,若∠B为锐角,BC∥DF,则∠B的大小为60°.