题目内容
如图，△ABC中，D，E两点分别在AB，AC上，且AD=12，DB=16，AE=16，EC=5．若M，N分别为DE和BC的中点，则AM：AN=考点：相似三角形的判定与性质
专题：
分析：求出AD=12，DB=16，AE=16，EC=5，根据相似三角形的判定判断出△ADE∽△ACB，再根据相似三角形的性质判断出AM：AN．
解答：解：∵AD=12，DB=16，AE=16，EC=5，
∴AB=AD+DB=12+16=28，AC=AE+EC=16+5=21，
∴
=
=
，
=
=
，
在△ADE和△ACB中，
=
，
又∵∠DAE=∠CAB，
∴△ADE∽△ACB，
又∵M，N分别为DE和BC的中点，
∴AM、AN分别为DE、BC边上的中线，
∴AM：AN=AD：AC=12：21=4：7．
故答案为4：7．
∴AB=AD+DB=12+16=28，AC=AE+EC=16+5=21，
∴
| AD |
| AC |
| 12 |
| 21 |
| 4 |
| 7 |
| AE |
| AB |
| 16 |
| 28 |
| 4 |
| 7 |
在△ADE和△ACB中，
| AD |
| AC |
| AE |
| AB |
又∵∠DAE=∠CAB，
∴△ADE∽△ACB，
又∵M，N分别为DE和BC的中点，
∴AM、AN分别为DE、BC边上的中线，
∴AM：AN=AD：AC=12：21=4：7．
故答案为4：7．
点评：本题考查了相似三角形的判定和性质，要知道，相似三角形对应中线的比等于相似比．
练习册系列答案
相关题目
如图，已知∠1=80°，∠2=100°，请判断直线AB与CD的位置关系，并用两种方法说明理由．
如图，∠B=62°，∠3=30°，∠4=88°，AB与CD平行吗？AD与BC平行吗？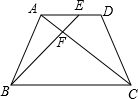
在等腰梯形ABCD中，AD∥CB，且AD=
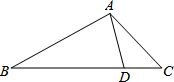如图，在△ABC中，AC=4，AB=6，BC=8，点D在BC边上，且CD=2，则AD的长为