题目内容
3.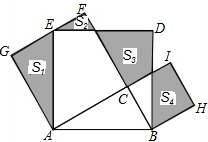 如图,Rt△ABC中,∠C=90°,AC=12,BC=5,分别以AB、AC、BC为边在AB的同侧作正方形ABDE、ACFG、BCIH,四块阴影部分的面积分别为S1、S2、S3、S4,则S1+S2+S3+S4等于( )
如图,Rt△ABC中,∠C=90°,AC=12,BC=5,分别以AB、AC、BC为边在AB的同侧作正方形ABDE、ACFG、BCIH,四块阴影部分的面积分别为S1、S2、S3、S4,则S1+S2+S3+S4等于( )| A. | 60 | B. | 90 | C. | 144 | D. | 169 |
分析 过D作BM的垂线交BM于N,通过证明S1+S2+S3+S4=Rt△ABC的面积×3,依此即可求解.
解答  解:过D作BM的垂线交BM于N,连接DI,
解:过D作BM的垂线交BM于N,连接DI,
∵图中S2=SRt△DOI,S△BOC=S△MND,
∴S2+S4=SRt△ABC.
可证明Rt△AGE≌Rt△ABC,Rt△DNB≌Rt△BHD,
∴S1+S2+S3+S4
=S1+S3+(S2+S4),
=Rt△ABC的面积+Rt△ABC的面积+Rt△ABC的面积
=Rt△ABC的面积×3
=12×5÷2×3
=90.
故选:B.
点评 本题考查勾股定理的知识,有一定难度,解题关键是将勾股定理和正方形的面积公式进行灵活的结合和应用.

练习册系列答案
相关题目
14.把分式$\frac{2x-y}{2x+y}$中的x、y都扩大到原来的4倍,则分式的值( )
| A. | 扩大到原来的8倍 | B. | 扩大到原来的4倍 | C. | 缩小到原来的$\frac{1}{4}$ | D. | 不变 |
11.下列是二元一次方程组的是( )
| A. | $\left\{\begin{array}{l}x-y=1\\ \frac{1}{x}+y=4\end{array}$ | B. | $\left\{\begin{array}{l}{x+y=4}\\{{x}^{2}+{y}^{2}=9}\end{array}\right.$ | ||
| C. | $\left\{\begin{array}{l}x+y=4\\ xy=4\end{array}$ | D. | $\left\{\begin{array}{l}3x+5y=25\\ x+10y=25\end{array}$ |
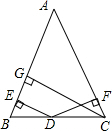 如图所示,已知在△ABC中,AB=AC,CG⊥AB,点D是BC边上的一点,DE⊥AB,DF⊥AC.
如图所示,已知在△ABC中,AB=AC,CG⊥AB,点D是BC边上的一点,DE⊥AB,DF⊥AC.