题目内容
2. 如图,点D是△ABC的边BC上任意一点,点E、F分别是线段AD、CE的中点,且△ABC的面积为28cm2,则△BEF的面积=7cm2.
如图,点D是△ABC的边BC上任意一点,点E、F分别是线段AD、CE的中点,且△ABC的面积为28cm2,则△BEF的面积=7cm2.
分析 根据三角形的中线把三角形分成两个面积相等的三角形解答.
解答 解:∵点E是AD的中点,
∴S△ABE=$\frac{1}{2}$S△ABD,S△ACE=$\frac{1}{2}$S△ADC,
∴S△ABE+S△ACE=$\frac{1}{2}$S△ABC=$\frac{1}{2}$×28=14,
∴S△BCE=$\frac{1}{2}$S△ABC=$\frac{1}{2}$×28=14,
∵点F是CE的中点,
∴S△BEF=$\frac{1}{2}$S△BCE=$\frac{1}{2}$×14=7.
故答案为:7cm2
点评 本题考查了三角形的面积,主要利用了三角形的中线把三角形分成两个面积相等的三角形,原理为等底等高的三角形的面积相等.

练习册系列答案
相关题目
10.下列根式中,最简二次根式是( )
| A. | $\sqrt{9a}$ | B. | $\sqrt{{a^2}+{b^2}}$ | C. | $\sqrt{\frac{a}{3}}$ | D. | $\sqrt{0.5}$ |
7.命题“垂直于同一条直线的两条直线互相平行”的题设是( )
| A. | 垂直 | B. | 两条直线 | ||
| C. | 同一条直线 | D. | 两条直线垂直于同一条直线 |
14.把分式$\frac{2x-y}{2x+y}$中的x、y都扩大到原来的4倍,则分式的值( )
| A. | 扩大到原来的8倍 | B. | 扩大到原来的4倍 | C. | 缩小到原来的$\frac{1}{4}$ | D. | 不变 |
11.下列是二元一次方程组的是( )
| A. | $\left\{\begin{array}{l}x-y=1\\ \frac{1}{x}+y=4\end{array}$ | B. | $\left\{\begin{array}{l}{x+y=4}\\{{x}^{2}+{y}^{2}=9}\end{array}\right.$ | ||
| C. | $\left\{\begin{array}{l}x+y=4\\ xy=4\end{array}$ | D. | $\left\{\begin{array}{l}3x+5y=25\\ x+10y=25\end{array}$ |
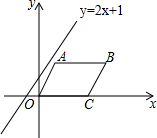 在平面直角坐标系中,?OABC的边OC落在x轴的正半轴上,且点C(4,0),B(6,2),直线y=2x+1以每秒1个单位的速度向下平移,经过6秒该直线可将□OABC的面积平分.
在平面直角坐标系中,?OABC的边OC落在x轴的正半轴上,且点C(4,0),B(6,2),直线y=2x+1以每秒1个单位的速度向下平移,经过6秒该直线可将□OABC的面积平分.