题目内容
4.某楼盘一楼是车库(暂不出售),二楼至二十三楼均为商品房(对外销售).商品房售价方案如下:第八层售价为3000元/米2,从第八层起每上升一层.每平方米的售价增加40元;反之,楼层每下降一层,每平方米的售价减少20元.已知商品房每套面积均为120平方米,开发商为购买者制定了两种购房方案:方案一:购买者先交纳首付金额(商品房总价的30%),再办理分期付款(即贷款).
方案二:购买者若一次付清所有房款,则享受8%的优惠,并免收五年物业管理费(已知每月物业管理费为a元).
(1)直接写出三楼售价为2900元/米2,二十楼售价为3480元/米2;
(2)请写出每平方米售价y(元/米2)与楼层x(2≤x≤23,x是正整数)之间的函数解析式;
(3)小张已筹到120000元,若用方案一购房,他可以购买哪些楼层的商品房呢?
(4)有人建议老王使用方案二购买第十六层,但他认为此方案还不如不免收物业管理费而直接享受9%的优惠划算.你认为老王的说法一定正确吗?请用具体数据阐明你的看法.
分析 (1)根据楼层的价格变化,可得答案;
(2)分类讨论:2≤x≤8,8<x≤23,根据楼层的价格变化,可得函数解析式;
(3)分类讨论:2≤x≤8,8<x≤23,根据首付款与筹备款的不等式关系,可得答案;
(4)根据方案二的方法,可得房款的关系式,再根据不免物业费直接享受9%的优惠,可得函数关系式,再根据不等式的关系,可得答案.
解答 解:(1)三楼售价为 2900 元/米2,二十楼售价为 3480 元/米2.
故答案为:2900,3480;
(2)每平方米售价y(元/米2)与楼层x(2≤x≤23,x是正整数)之间的函数解析式为y=$\left\{\begin{array}{l}{20x+2840(2≤x≤8)}\\{40x+2680(8<x≤23)}\end{array}\right.$;
(3)由(2)得当2≤x≤8时,(20x+2840)×120×30%=36(20x+2840)=36(20×8+2840)=108000<120000,
则2楼到8楼的楼层可任意选;
当8<x≤23时,(40x+2680)××30%=36(40x+2680)≤120000,
x<$\frac{49}{3}$,x是正整数,
8<x≤16,9层到6层任意楼层都可以购买,
综上所述,用方案一购房,他可以任意购买2层到16楼层的商品房;
(4)方案二y1=(40×16+2680)×120×(1-8%),
老王的想法y2=(40×16+2680)×120×(1-9%)+12×5a,
y1-y2=3984-60a,
当y1>y2时,即y1-y2=3984-60a>0,
0<a<60.4,想法正确,
当y1<y2时,y1-y2=3984-60a<0,
a>60.4,想法不正确,
因此,老王的说法不一定正确.
点评 本题考查的是用一次函数解决实际问题,读懂题目信息,找出数量关系表示出各楼层的单价以及是交房款的关系式是解题的关键.

 同步练习强化拓展系列答案
同步练习强化拓展系列答案| A. | 10$\sqrt{5}$ | B. | 11$\sqrt{5}$ | C. | 12$\sqrt{5}$ | D. | 13$\sqrt{5}$ |
| A. | x2+x4=x6 | B. | 2xy+3xy=5xy | C. | (x3)2=x6 | D. | x6÷x3=x3 |
| A. | 2012 | B. | -2012 | C. | $\frac{1}{2012}$ | D. | $-\frac{1}{2012}$ |
 如图,AD∥BC,BD⊥BC,若∠ABD=25°,求∠A的度数.
如图,AD∥BC,BD⊥BC,若∠ABD=25°,求∠A的度数. 如图,在△ABC中,CD⊥AB,垂直为点D,F为BC上一点,FG⊥AB,垂足为点G,E为AC上一点,连结DE,且∠1=∠2,求证:DE∥BC.
如图,在△ABC中,CD⊥AB,垂直为点D,F为BC上一点,FG⊥AB,垂足为点G,E为AC上一点,连结DE,且∠1=∠2,求证:DE∥BC.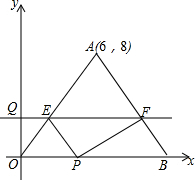 如图,△OAB的一边OB在x轴的正半轴上,点A的坐标为(6,8),OA=OB,点P在线段OB上,点Q在y轴的正半轴上,OP=2OQ,过点Q作x轴的平行线分别交OA,AB于点E,F.
如图,△OAB的一边OB在x轴的正半轴上,点A的坐标为(6,8),OA=OB,点P在线段OB上,点Q在y轴的正半轴上,OP=2OQ,过点Q作x轴的平行线分别交OA,AB于点E,F.