题目内容
14.已知△ABC的两边的长分别为2$\sqrt{5}$,5$\sqrt{5}$,则△ABC的周长不可能是( )| A. | 10$\sqrt{5}$ | B. | 11$\sqrt{5}$ | C. | 12$\sqrt{5}$ | D. | 13$\sqrt{5}$ |
分析 根据三角形两边之和大于第三边,两边之差小于第三边,先确定周长的范围即可解决问题.
解答 解:设三角形的另一边长为x,
根据三角形三边关系可知:x<2$\sqrt{5}$+3$\sqrt{5}$,即x<5$\sqrt{5}$,
x>3$\sqrt{5}$-2$\sqrt{5}$,即x>$\sqrt{5}$,
则$\sqrt{5}$<x<5$\sqrt{5}$,
其周长L要满足:$\sqrt{5}$+2$\sqrt{5}$+5$\sqrt{5}$<L<2$\sqrt{5}$+5$\sqrt{5}$+5$\sqrt{5}$,即9$\sqrt{5}$<L<12$\sqrt{5}$.
故选D.
点评 本题考查二次根式的应用、三角形三边关系定理,正确应用三角形三边关系定理是解决问题的关键,属于中考常考题型.

练习册系列答案
 金牌课堂练系列答案
金牌课堂练系列答案 三新快车金牌周周练系列答案
三新快车金牌周周练系列答案
相关题目
9.如图1所示,将一个正四棱锥(底面为正方形,四条测棱相等)的其中四条边剪开,得到图2,则被剪开的四条边有可能是( )
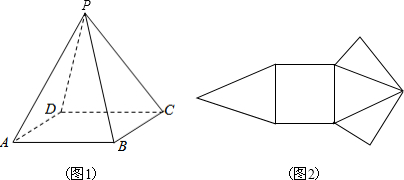

| A. | PA,PB,AD,BC | B. | PD,DC,BC,AB | C. | PA,AD,PC,BC | D. | PA,PB,PC,AD |
3.实数-2的相反数是( )
| A. | 2 | B. | -2 | C. | 0.5 | D. | -0.5 |
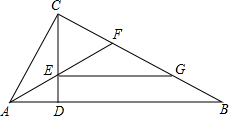 如图,在Rt△ABC中,∠ACB=90°,CD⊥AB于D点,AF平分∠BAC交CD于E点,交BC于F点,EG∥AB交BC于G点.
如图,在Rt△ABC中,∠ACB=90°,CD⊥AB于D点,AF平分∠BAC交CD于E点,交BC于F点,EG∥AB交BC于G点.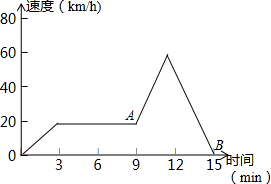 根据图回答下列问题:
根据图回答下列问题: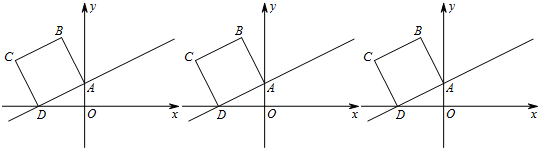
 为筹备2014年元旦晚会,同学们设计了一个圆筒形灯罩,底色漆成白色,然后缠绕红色油纸,如图所示,已知圆筒高108cm,其横截面周长为36cm,如果在圆筒表面恰好能缠绕油纸4圈,应至少裁剪180cm的油纸.
为筹备2014年元旦晚会,同学们设计了一个圆筒形灯罩,底色漆成白色,然后缠绕红色油纸,如图所示,已知圆筒高108cm,其横截面周长为36cm,如果在圆筒表面恰好能缠绕油纸4圈,应至少裁剪180cm的油纸.