题目内容
(1)有160个零件,平均分配给甲、乙两个车间加工,乙车间因另有紧急任务,所以在甲车间加工3小时后才开始加工,因此比甲车间迟20分钟完成,已知甲、乙两车间的生产效率的比是1:3,则甲、乙两车间每小时各能加工多少零件?
(2)如果零件总数为a件,其它条件不变,你能求出甲、乙两个车间的生产时间吗?并用含a的代数式表示甲、乙两车间每小时各能加工多少零件.
(2)如果零件总数为a件,其它条件不变,你能求出甲、乙两个车间的生产时间吗?并用含a的代数式表示甲、乙两车间每小时各能加工多少零件.
考点:分式方程的应用,一元一次方程的应用
专题:
分析:(1)设甲每小时加工x个零件,乙每小时加工3x个零件,由工程问题的数量关系工作时间=工作总量÷工作效率建立方程求出其解即可;
(2)设甲每小时加工y个零件,乙每小时加工3y个零件,由工程问题的数量关系工作时间=工作总量÷工作效率建立方程求出其解即可;
(2)设甲每小时加工y个零件,乙每小时加工3y个零件,由工程问题的数量关系工作时间=工作总量÷工作效率建立方程求出其解即可;
解答:解:设甲每小时加工x个零件,乙每小时加工3x个零件,由题意,得
-
=3-
,
解得:x=20,
经检验,x=20是原方程的解.
∴乙每小时加工60个零件.
答:甲每小时加工20个零件,乙每小时加工60个零件;
(2)设甲每小时加工y个零件,乙每小时加工3y个零件,由题意,得
-
=3-
,
解得:y=
a,
经检验,y=
a是原方程的解.
∴乙每小时加工
a个零件.
∴甲的生产时间为:
÷
a=4小时,
乙的生产时间为:
÷
a=
小时
答:甲需要4小时,乙要
小时. 甲每小时加工零件
a个,乙每小时加工零件
a个.
| 80 |
| x |
| 80 |
| 3x |
| 1 |
| 3 |
解得:x=20,
经检验,x=20是原方程的解.
∴乙每小时加工60个零件.
答:甲每小时加工20个零件,乙每小时加工60个零件;
(2)设甲每小时加工y个零件,乙每小时加工3y个零件,由题意,得
| ||
| y |
| ||
| 3y |
| 1 |
| 3 |
解得:y=
| 1 |
| 8 |
经检验,y=
| 1 |
| 8 |
∴乙每小时加工
| 3 |
| 8 |
∴甲的生产时间为:
| a |
| 2 |
| 1 |
| 8 |
乙的生产时间为:
| a |
| 2 |
| 3 |
| 8 |
| 4 |
| 3 |
答:甲需要4小时,乙要
| 4 |
| 3 |
| 1 |
| 8 |
| 3 |
| 8 |
点评:本题考查了列分式方程解实际问题的运用,分式方程的解法的运用,代数式的运用,工程问题的数量关系工作时间=工作总量÷工作效率的运用,解答时根据工程问题的数量关系建立方程是关键.

练习册系列答案
相关题目
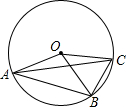 如图,OA,OB,OC都是⊙O的半径,若∠AOB是锐角,且∠AOB=2∠BOC.则下列结论正确的是( )
如图,OA,OB,OC都是⊙O的半径,若∠AOB是锐角,且∠AOB=2∠BOC.则下列结论正确的是( )| A、AB=2BC |
| B、AB<2BC |
| C、∠AOB=2∠CAB |
| D、∠ACB=4∠CAB |
 2014年3月8日凌晨,马来西亚航空公司MH370航班与总部失去联系,我国随即针对该航班展开了大规模搜救行动,我国的侦察机和搜救船在某海域同时沿同一方向配合搜寻(如图13).在距海面900米的高空A处,侦察机测得搜救船在俯角为30°的海面C处,当侦察机以150
2014年3月8日凌晨,马来西亚航空公司MH370航班与总部失去联系,我国随即针对该航班展开了大规模搜救行动,我国的侦察机和搜救船在某海域同时沿同一方向配合搜寻(如图13).在距海面900米的高空A处,侦察机测得搜救船在俯角为30°的海面C处,当侦察机以150 如图所示,花都区某学校准备在教学楼后面搭建一个简易矩形自行车车棚,一边利用教学楼的后墙(可利用的墙为19m),另外三边利用学校现有总长38m的铁栏围成.若围成的面积为180m2,试求出自行车车棚的长和宽.
如图所示,花都区某学校准备在教学楼后面搭建一个简易矩形自行车车棚,一边利用教学楼的后墙(可利用的墙为19m),另外三边利用学校现有总长38m的铁栏围成.若围成的面积为180m2,试求出自行车车棚的长和宽.