题目内容
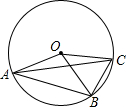 如图,OA,OB,OC都是⊙O的半径,若∠AOB是锐角,且∠AOB=2∠BOC.则下列结论正确的是( )
如图,OA,OB,OC都是⊙O的半径,若∠AOB是锐角,且∠AOB=2∠BOC.则下列结论正确的是( )| A、AB=2BC |
| B、AB<2BC |
| C、∠AOB=2∠CAB |
| D、∠ACB=4∠CAB |
考点:圆心角、弧、弦的关系,三角形三边关系
专题:
分析:首先取
的中点D,连接AD,BD,由∠AOB=2∠BOC,易得AD=BD=BC,继而证得AB<2BC,又由圆周角定理,可得∠AOB=4∠CAB,∠ACB=∠BOC=2∠CAB.
 |
| AB |
解答: 解:取
解:取
的中点D,连接AD,BD,
∵∠AOB=2∠BOC,
∴
=2
,
∴
=
=
,
∴AD=BD=BC,
∵AB<AD+BD,
∴AB<2BC.故A错误,B正确;
∵∠AOB=2∠BOC,∠BOC=2∠CAB,
∴∠AOB=4∠CAB;故C错误;
∵∠AOB=2∠ACB,
∴∠ACB=∠BOC=2∠CAB,故D错误.
故选B.
 解:取
解:取 |
| AB |
∵∠AOB=2∠BOC,
∴
 |
| AB |
 |
| BC |
∴
 |
| AD |
 |
| BD |
 |
| BC |
∴AD=BD=BC,
∵AB<AD+BD,
∴AB<2BC.故A错误,B正确;
∵∠AOB=2∠BOC,∠BOC=2∠CAB,
∴∠AOB=4∠CAB;故C错误;
∵∠AOB=2∠ACB,
∴∠ACB=∠BOC=2∠CAB,故D错误.
故选B.
点评:此题考查了弧、弦与圆心角的关系以及圆周角定理.此题难度适中,注意掌握辅助线的作法,注意掌握数形结合思想的应用.

练习册系列答案
相关题目
 如图,将一个直角三角形板AOB的顶点O放在直线CD上,若∠AOC=35°,则∠BOD等于( )
如图,将一个直角三角形板AOB的顶点O放在直线CD上,若∠AOC=35°,则∠BOD等于( )| A、155° | B、145° |
| C、65° | D、55° |
 一个几何体的形状如图所示,它的左视图是( )
一个几何体的形状如图所示,它的左视图是( )A、 |
B、 |
C、 |
D、 |
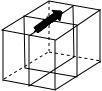 小明制作了一个正方体包装盒,他在这个正方体包装盒的上面设计了一个“
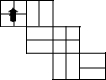
小明制作了一个正方体包装盒,他在这个正方体包装盒的上面设计了一个“ ”标志,并在正方体的每个表面都画了黑色粗线,如图所示在下列图形中,是这个正方体包装盒的表面展开图的是( )
”标志,并在正方体的每个表面都画了黑色粗线,如图所示在下列图形中,是这个正方体包装盒的表面展开图的是( )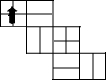

 在Rt△ABC中,∠C=90°,∠BDC=45°,BC=1,DA=
在Rt△ABC中,∠C=90°,∠BDC=45°,BC=1,DA=