题目内容
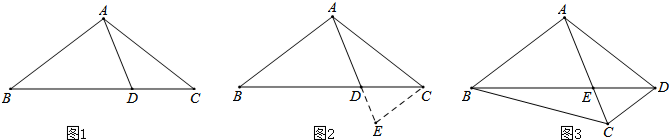
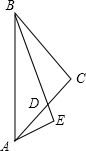
12.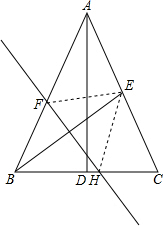 如图,在△ABC中,AB=AC,底边BC上的高AD=12,tan C=2,如果将△ABC沿直线l翻折后,点B刚好落在AC边的中点E处,直线l与边AB交于点F,与边BC交于点H,求BH的长.
如图,在△ABC中,AB=AC,底边BC上的高AD=12,tan C=2,如果将△ABC沿直线l翻折后,点B刚好落在AC边的中点E处,直线l与边AB交于点F,与边BC交于点H,求BH的长.
分析 过点E作EG⊥BC,垂足为G,先根据点B刚好落在AC边的中点E处得出EG是△ACD的中位线,再由tanC=2得出DC即CG的长,设BH=x,则HE=BH=x,HG=9-x,在Rt△EGH中,EH2=EG2+HG2,根据勾股定理即可得出x的值,进而得出结论.
解答 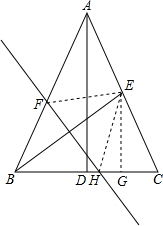 解:过点E作EG⊥BC,垂足为G,
解:过点E作EG⊥BC,垂足为G,
又∵AB=AC,AE=EC,AD=12,
∴BD=DC,EG=$\frac{1}{2}$AD=6,DG=GC,
∵tanC=$\frac{EG}{CG}$=$\frac{AD}{CD}$=2,
∴DC=6,CG=3,
设BH=x,则HE=BH=x,HG=9-x,
在Rt△EGH中,EH2=EG2+HG2,即x2=62+(9-x)2,
解得x=6.5.
点评 本题考查的是翻折变换,根据题意作出辅助线,构造出三角形的中位线,再根据勾股定理求解是解答此题的关键.

练习册系列答案
 金钥匙试卷系列答案
金钥匙试卷系列答案
相关题目
20.-2015的相反数是( )
| A. | 2015 | B. | $\frac{1}{2015}$ | C. | -$\frac{1}{2015}$ | D. | -2015 |
1.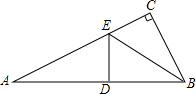 如图,在△ABC中,∠C=90°,沿过点B的一条直线BE,折叠△ABC,使点C恰好落在AB边的中点D处,则∠A的度数是( )
如图,在△ABC中,∠C=90°,沿过点B的一条直线BE,折叠△ABC,使点C恰好落在AB边的中点D处,则∠A的度数是( )
 如图,在△ABC中,∠C=90°,沿过点B的一条直线BE,折叠△ABC,使点C恰好落在AB边的中点D处,则∠A的度数是( )
如图,在△ABC中,∠C=90°,沿过点B的一条直线BE,折叠△ABC,使点C恰好落在AB边的中点D处,则∠A的度数是( )| A. | 20° | B. | 30° | C. | 40° | D. | 45° |
 如图,△ABC中,BC=AC,∠ACB=90°,BD平分∠ABC,AE⊥BD,交BD延长线于E,
如图,△ABC中,BC=AC,∠ACB=90°,BD平分∠ABC,AE⊥BD,交BD延长线于E,