题目内容
5.一个圆柱体包装盒,高40cm,底面周长20cm.现将彩色矩形纸带AMCN裁剪成一个平行四边形ABCD(如图1),然后用这条平行四边形纸带按如图2的方式把这个圆柱体包装盒的侧面进行包贴(要求包贴时没有重叠部分),纸带在侧面缠绕四圈,正好将这个圆柱体包装盒的侧面全部包贴满,则所需的纸带AD的长度为20$\sqrt{13}$ cm.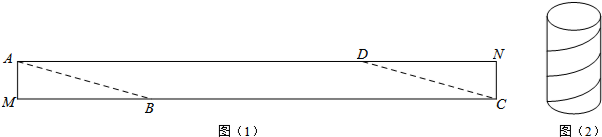
分析 根据圆柱体包装盒,高40cm,纸带在侧面缠绕四圈,正好将这个圆柱包装盒的侧面全部包贴满,可得出BF,AB的长度,由勾股定理得到AF的长度,即可得到结果.
解答 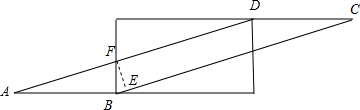 解:根据包贴方法可得展开图如下:
解:根据包贴方法可得展开图如下:
过点F作FE⊥BC于E,
∵纸带在侧面缠绕四圈,正好将这个三棱柱包装盒的侧面全部包贴满,
∵圆柱体的高40cm,
∴FB=$\frac{40}{3}$cm,AB=20,
在Rt△ABF中,AF=$\frac{20\sqrt{13}}{3}$,
∵DF=2AF=$\frac{40\sqrt{13}}{3}$,
∴AD=AF+DF=20$\sqrt{13}$,
故答案为;20$\sqrt{13}$.
点评 本题考查了平面展开图形的运用.关键是明确立体图形与其平面展开图形之间的数量关系,充分运用勾股定理及三角函数的定义解题.

练习册系列答案
相关题目
13.为调查某班学生每天使用零花钱的情况,张华随机调查了20名同学,结果如下表:
则这20名同学每天使用的零花钱的众数和中位数分别是( )
| 每天使用零花钱(单位:元) | 1 | 2 | 3 | 4 | 5 |
| 人数 | 1 | 3 | 6 | 5 | 5 |
| A. | 3,3 | B. | 3,3.5 | C. | 3.5,3.5 | D. | 3.5,3 |
14.在刚刚过去的2014年,中央财政下达农村义务教育经费保障机制资金共878.97亿元,在学生人数减少的情况下,仍比2013年增长6.1%.数据“878.97亿元”用科学记数法可表示为( )
| A. | 878.97×108元 | B. | 878.97×109元 | C. | 8.7897×1010元 | D. | 8.7897×1011元 |
11.设函数y=x+5与$y=\frac{3}{x}$的图象的两个交点的横坐标为a、b,则$\frac{1}{a}+\frac{1}{b}$的值是( )
| A. | $-\frac{5}{3}$ | B. | $\frac{5}{3}$ | C. | $-\frac{3}{5}$ | D. | $\frac{3}{5}$ |
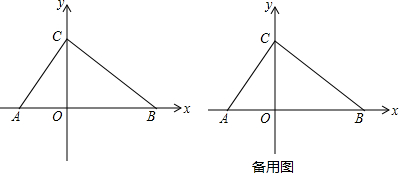
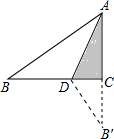 如图,在△ABC中,AB=20,AC=12,BC=16,把△ABC折迭,使AB落在直线AC上,则重迭部分(阴影部分)的面积是36.
如图,在△ABC中,AB=20,AC=12,BC=16,把△ABC折迭,使AB落在直线AC上,则重迭部分(阴影部分)的面积是36.