题目内容
18.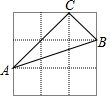 如图,在3×3的正方形网格中,每个小正方形的边长都为1,△ABC的三个顶点均在格点上,则AB边上的高为( )
如图,在3×3的正方形网格中,每个小正方形的边长都为1,△ABC的三个顶点均在格点上,则AB边上的高为( )| A. | $\frac{2\sqrt{10}}{5}$ | B. | $\frac{\sqrt{10}}{5}$ | C. | $\frac{\sqrt{10}}{10}$ | D. | $\frac{3\sqrt{10}}{10}$ |
分析 首先,根据勾股定理求得△ABC各边的长度;然后,根据勾股定理逆定理推知△ABC是直角三角形;最后,根据面积法来求△ABC中AB边上的高.
解答 解:设△ABC中AB边上的高为h.
∵AB2=10,AC2=8,BC2=2,
∴AB2=AC2+BC2,
∴∠ACB=90°,
S△ABC=$\frac{1}{2}$BC•AC=$\frac{1}{2}$AB•h,即$\frac{1}{2}$×$\sqrt{2}$×2$\sqrt{2}$=$\frac{1}{2}$×$\sqrt{10}$h.
解得,h=$\frac{2\sqrt{10}}{5}$.
故选A.
点评 本题考查了勾股定理,勾股定理的逆定理,直角三角形面积的计算.勾股定理应用的前提条件是在直角三角形中.

练习册系列答案
相关题目
8.四边形ABCD的对角线AC、BD交于点O,有以下结论:①AB=BC;②∠DAB=90°;③BO=DO,AO=CO;④四边形ABCD是矩形;⑤四边形ABCD是菱形;⑥四边形ABCD是正方形.下列推论不正确的是( )
| A. | 由②③,得④ | B. | 由①③,得⑤ | C. | 由①②,得⑥ | D. | 由①④,得⑥ |
9.关于x的不等式组$\left\{\begin{array}{l}{x-a≥0}\\{3-2x>-1}\end{array}\right.$的整数解共有5个,则a的取值范围( )
| A. | a=-3 | B. | -4<a<-3 | C. | -4≤a<-3 | D. | -4<a≤-3 |
3.在平面直角坐标系中,点P的坐标是(3,-2),则点P到x轴的距离为( )
| A. | 2 | B. | 3 | C. | -2 | D. | -3 |
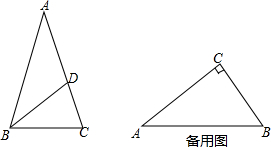 我们知道,三角形的内心是三条角平分线的交点,过三角形内心的一条直线与两边相交,两交点之间的线段把这个三角形分成两个图形.若有一个图形与原三角形相似,则把这条线段叫做这个三角形的“內似线”.
我们知道,三角形的内心是三条角平分线的交点,过三角形内心的一条直线与两边相交,两交点之间的线段把这个三角形分成两个图形.若有一个图形与原三角形相似,则把这条线段叫做这个三角形的“內似线”.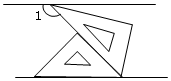 如图,将一副三角板和一张对边平行的纸条按下列方式摆放:含30°角的直角三角板的斜边与含45°角的直角三角板一直角边重合,含45°角的直角三角板的斜边与纸条一边重合,含30°角的三角板的一个顶点在纸条的另一边上,则∠1的度数是135°.
如图,将一副三角板和一张对边平行的纸条按下列方式摆放:含30°角的直角三角板的斜边与含45°角的直角三角板一直角边重合,含45°角的直角三角板的斜边与纸条一边重合,含30°角的三角板的一个顶点在纸条的另一边上,则∠1的度数是135°.
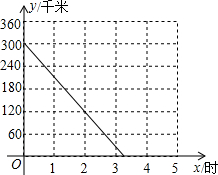 A、B两座城市之间有一条高速公路,甲、乙两辆汽车同时分别从这条公路两端的入口处驶入,并始终在高速公路上正常行驶.甲车驶住B城,乙车驶往A城,甲车在行驶过程中速度始终不变,甲车距B城高速公路入口处的距离y(km)与行驶时间x(h)之间的关系如图.
A、B两座城市之间有一条高速公路,甲、乙两辆汽车同时分别从这条公路两端的入口处驶入,并始终在高速公路上正常行驶.甲车驶住B城,乙车驶往A城,甲车在行驶过程中速度始终不变,甲车距B城高速公路入口处的距离y(km)与行驶时间x(h)之间的关系如图.