题目内容
14.问题情境:在学完2.4节圆周角之后,老师出了这样一道题:如图1,已知点A为∠MPN的平分线PQ上的任一点,以AP为弦作圆O与边PM、PN分别交于B、C两点,连结AB、BC、CA,形成了圆O的内接△ABC.小明同学发现△ABC是一个等腰三角形,理由是∠ABC=∠APC,∠ACB=∠APB,又由角平分线得∠APC=∠APB,所以∠ABC=∠ACB,AB=AC得证.
请你说出小明使用的是圆周角的哪个性质:同弧所对的圆周角相等(只写文字内容).
深入探究:爱钻研的小慧却画出了图2,与边PN的反向延长线交于点C,其它条件不变,△ABC仍是等腰三角形,请你写出证明过程.
拓展提高:妙想的小聪提出如图3,如果圆O与边PN相切于点C(与P点已重合),其它条件不变,△ABC仍是等腰三角形吗?若是,请写出证明过程;若不是,请说明理由.

分析 因为∠ABC和∠APC都是弧AC对着的圆周角,所以∠ABC=∠APC,即同弧所对的圆周角相等,同理可得∠ACB=∠APB,进而可知道小明使用的是圆周角的哪个性质;
深入探究:△ABC仍是等腰三角形,由圆的内接四边形定理以及圆周角定理证明再结合已知条件证明∠ABC=∠ACB即可得到AB=AC;
拓展提高:作直径CH,连结AH,由圆周角定理以及其同理和切线的性质定理再结合已知条件证明∠ABC=∠ACB,即可得到AB=AC.
解答 解:问题情境:同弧所对的圆周角相等,
深入探究:△ABC仍是等腰三角形,理由如下:
∵∠ABC+∠APC=180°,∠APN+∠APC=180°,
∴∠ABC=∠APN.
∵PA 平分∠MPN,
∴∠APB=∠APN,
∴∠ABC=∠APB.
而∠APB=∠ACB,
∴∠ABC=∠ACB,
∴AB=AC;
拓展提高:△ABC仍是等腰三角形理由如下:
作直径CH,连结AH,
∵CH为直径,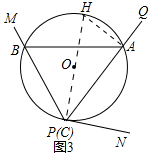
∴∠AHC=90°,
∴∠H+∠ACH=90°.
∵CN与圆O相切,
∴CN⊥CH,
∴∠ACN+∠ACH=90°,
∴∠ACN=∠H.
∵∠ABC=∠H,
∴∠ACN=∠ABC.
∵PA 平分∠MPN,
∴∠ACB=∠CAN.
∴∠ABC=∠ACB,
∴AB=AC.
点评 本题考查了和圆有关的综合性题目,用到的知识点有圆周角定义及其推论、角平分线的定义、圆的内接四边形定理以及切线的性质定理,题目的设计新颖,对学生理解问题的能力要求较高,特别是拓展提高部分正确作出图形的辅助线是解题关键.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
9.(-8)2的立方根是( )
| A. | -2 | B. | ±2 | C. | 4 | D. | ±4 |
6.已知数据$\sqrt{3}$,$\frac{1}{3}$,$\sqrt{2}$,π,-3.14,其中无理数出现的频率为( )
| A. | 80% | B. | 60% | C. | 40% | D. | 20% |
3.如果a2-ab-4c是一个完全平方式,那么c等于( )
| A. | $\frac{1}{4}$b2 | B. | -$\frac{1}{8}$b2 | C. | $\frac{1}{16}$b2 | D. | -$\frac{1}{16}$b2 |
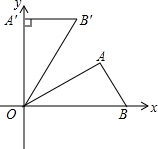 如图,在平面直角坐标系中,Rt△OAB的斜边OB在x轴的正半轴上,点A在第一象限,将△OAB,使点O按逆时针方向旋转至△OA′B′,使点A的对应点A′落在y轴的正半轴上,已知OB=2,∠AOB=30°.
如图,在平面直角坐标系中,Rt△OAB的斜边OB在x轴的正半轴上,点A在第一象限,将△OAB,使点O按逆时针方向旋转至△OA′B′,使点A的对应点A′落在y轴的正半轴上,已知OB=2,∠AOB=30°.
 如图,已知第一象限内的点A在反比例函数y=$\frac{\sqrt{6}}{x}$上,第二象限的点B在反比例函数y=$\frac{k}{x}$上,且OA⊥OB,∠A=30°,则k的值为-$\frac{\sqrt{6}}{3}$.
如图,已知第一象限内的点A在反比例函数y=$\frac{\sqrt{6}}{x}$上,第二象限的点B在反比例函数y=$\frac{k}{x}$上,且OA⊥OB,∠A=30°,则k的值为-$\frac{\sqrt{6}}{3}$.