题目内容
8.某水果基地计划装运甲、乙、丙三种水果到外地销售(每辆汽车规定满载,并且只装一种水果).如表为装运甲、乙、丙三种水果的重量及利润.| 甲 | 乙 | 丙 | |
| 每辆汽车能装的数量(吨) | 4 | 2 | 3 |
| 每吨水果可获利润(千元) | 5 | 7 | 4 |
(2)水果基地计划用20辆汽车装运甲、乙、丙三种水果共72吨到B地销售(每种水果不少于一车),假设装运甲水果的汽车为m辆,则装运乙、丙两种水果的汽车各多少辆?(结果用m表示)
(3)在(2)问的基础上,如何安排装运可使水果基地获得最大利润?最大利润是多少?
分析 (1)根据“8辆汽车装运乙、丙两种水果共22吨到A地销售”列出方程组,即可解答;
(2)设装运乙、丙水果的车分别为a辆,b辆,列出方程组$\left\{\begin{array}{l}{m+a+b=20}\\{4m+2a+3b=72}\end{array}\right.$,即可解答;
(3)设总利润为w千元,表示出w=10m+216.列出不等式组$\left\{\begin{array}{l}{m≥1}\\{m-12≥1}\\{32-2m≥1}\end{array}\right.$,确定m的取值范围13≤m≤15.5,结合一次函数的性质,即可解答.
解答 解:(1)设装运乙、丙水果的车分别为x辆,y辆,得:
$\left\{\begin{array}{l}{x+y=8}\\{2x+3y=22}\end{array}\right.$,
解得:$\left\{\begin{array}{l}{x=2}\\{y=6}\end{array}\right.$.
答:装运乙种水果的车有2辆、丙种水果的汽车有6辆.
(2)设装运乙、丙水果的车分别为a辆,b辆,得:
$\left\{\begin{array}{l}{m+a+b=20}\\{4m+2a+3b=72}\end{array}\right.$,
解得$\left\{\begin{array}{l}{a=m-12}\\{b=32-2m}\end{array}\right.$.
答:装运乙种水果的汽车是(m-12)辆,丙种水果的汽车是(32-2m)辆.
(3)设总利润为w千元,
w=5×4m+7×2(m-12)+4×3(32-2m)=10m+216.
∵$\left\{\begin{array}{l}{m≥1}\\{m-12≥1}\\{32-2m≥1}\end{array}\right.$,
∴13≤m≤15.5,
∵m为正整数,
∴m=13,14,15,
在w=10m+216中,w随x的增大而增大,
∴当m=15时,W最大=366(千元),
答:当运甲水果的车15辆,运乙水果的车3辆,运丙水果的车2辆,利润最大,最大利润为366千元.
点评 此题主要考查了一次函数的应用,解决本题的关键是运用函数性质求最值需确定自变量的取值范围.

| A. | 2 | B. | -2 | C. | $\frac{1}{2}$ | D. | -$\frac{1}{2}$ |
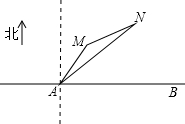 如图,公路AB为东西走向,在点A北偏东36.5°方向上,距离5千米处是村庄M;在点A北偏东53.5°方向上,距离10千米处是村庄N(参考数据;sin36.5°=0.6,cos36.5°=0.8,tan36.5°=0.75,sin23.6°=0.4,cos66.4°=0.4,tan21.8°=0.4).
如图,公路AB为东西走向,在点A北偏东36.5°方向上,距离5千米处是村庄M;在点A北偏东53.5°方向上,距离10千米处是村庄N(参考数据;sin36.5°=0.6,cos36.5°=0.8,tan36.5°=0.75,sin23.6°=0.4,cos66.4°=0.4,tan21.8°=0.4).
 如图,?ABCD的对角线AC、BD交于点O,EF过点O且与BC、AD分别交于点E、F.试猜想线段AE、CF的关系,并说明理由.
如图,?ABCD的对角线AC、BD交于点O,EF过点O且与BC、AD分别交于点E、F.试猜想线段AE、CF的关系,并说明理由. 我们知道:光反射时,反射光线、入射光线和法线在同一平面内,反射光线、入射光线分别在法线两侧,反射角等于入射角.如右图,AO为入射光线,入射点为O,ON为法线(过入射点O且垂直于镜面的直线),OB为反射光线,此时反射角∠BON等于入射角∠AON.
我们知道:光反射时,反射光线、入射光线和法线在同一平面内,反射光线、入射光线分别在法线两侧,反射角等于入射角.如右图,AO为入射光线,入射点为O,ON为法线(过入射点O且垂直于镜面的直线),OB为反射光线,此时反射角∠BON等于入射角∠AON.

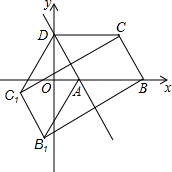 如图,已知?ABCD的三个顶点A(n,0)、B(m,0)、D(0,2n)(m>n>0),作?ABCD关于直线AD的对称图形AB1C1D
如图,已知?ABCD的三个顶点A(n,0)、B(m,0)、D(0,2n)(m>n>0),作?ABCD关于直线AD的对称图形AB1C1D