题目内容
18.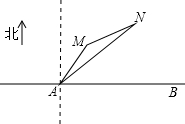 如图,公路AB为东西走向,在点A北偏东36.5°方向上,距离5千米处是村庄M;在点A北偏东53.5°方向上,距离10千米处是村庄N(参考数据;sin36.5°=0.6,cos36.5°=0.8,tan36.5°=0.75,sin23.6°=0.4,cos66.4°=0.4,tan21.8°=0.4).
如图,公路AB为东西走向,在点A北偏东36.5°方向上,距离5千米处是村庄M;在点A北偏东53.5°方向上,距离10千米处是村庄N(参考数据;sin36.5°=0.6,cos36.5°=0.8,tan36.5°=0.75,sin23.6°=0.4,cos66.4°=0.4,tan21.8°=0.4).(1)求M,N两村之间的距离;
(2)试问村庄N在村庄M的什么方向上?(精确到0.1度)
分析 (1)过点M作CD∥AB,NE⊥AB,在Rt△ACM中求出CM,AC,在Rt△ANE中求出NE,AE,继而得出MD,ND的长度,在Rt△MND中利用勾股定理可得出MN的长度.
(2)在Rt△MND中,根据tan∠NMD=$\frac{ND}{MD}$=$\frac{2}{5}$=0.4km,再根据tan21.8°=0.4,得出∠NMD=21.8°,再根据∠MND=90°-∠NMD,即可得出村庄N在村庄M的北偏东68.2°方向上.
解答  解:过点M作CD∥AB,NE⊥AB,如图:
解:过点M作CD∥AB,NE⊥AB,如图:
在Rt△ACM中,∠CAM=36.5°,AM=5km,
∵sin36.5°=$\frac{CM}{5}$=0.6,
∴CM=3,AC=$\sqrt{A{M}^{2}-C{M}^{2}}$=4km,
在Rt△ANE中,∠NAE=90°-53.5°=36.5°,AN=10km,
∵sin36.5°=$\frac{NE}{10}$=0.6,
∴NE=6,AE=$\sqrt{A{N}^{2}-N{E}^{2}}$=8km,
∴MD=CD-CM=AE-CM=5km,ND=NE-DE=NE-AC=2km,
在Rt△MND中,MN=$\sqrt{M{D}^{2}+N{D}^{2}}$=$\sqrt{29}$(km).
(2)在Rt△MND中,tan∠NMD=$\frac{ND}{MD}$=$\frac{2}{5}$=0.4(km),
∴∠NMD=21.8°,
∴∠MND=90°-21.8°=68.2°,
∴村庄N在村庄M的北偏东68.2°方向上.
点评 本题考查了解直角三角形的知识,解答本题的关键是构造直角三角形,利用三角函数值求解相关线段的长度,难度较大.

练习册系列答案
 口算题卡加应用题集训系列答案
口算题卡加应用题集训系列答案 综合自测系列答案
综合自测系列答案
相关题目
8. 如图,已知四边形ABEC内接于⊙O,点D在AC的延长线上,CE平分∠BCD交⊙O于点E,则下列结论中一定正确的是( )
如图,已知四边形ABEC内接于⊙O,点D在AC的延长线上,CE平分∠BCD交⊙O于点E,则下列结论中一定正确的是( )
 如图,已知四边形ABEC内接于⊙O,点D在AC的延长线上,CE平分∠BCD交⊙O于点E,则下列结论中一定正确的是( )
如图,已知四边形ABEC内接于⊙O,点D在AC的延长线上,CE平分∠BCD交⊙O于点E,则下列结论中一定正确的是( )| A. | AB=AE | B. | AB=BE | C. | AE=BE | D. | AB=AC |
9.生物学家发现一种病毒的长度约为0.00000402毫米,数据0.00000402用科学记数法表示( )
| A. | 0.402×10-5 | B. | 4.02×10-6 | C. | 4.02×10-7 | D. | 40.2×10-7 |
13.某初中决定从三名男生和两名女生中选出两名同学担任校艺术节文艺演出专场的主持人,则选出的恰为一男一女的概率是( )
| A. | $\frac{1}{5}$ | B. | $\frac{2}{5}$ | C. | $\frac{3}{5}$ | D. | $\frac{4}{5}$ |
8.某水果基地计划装运甲、乙、丙三种水果到外地销售(每辆汽车规定满载,并且只装一种水果).如表为装运甲、乙、丙三种水果的重量及利润.
(1)用8辆汽车装运乙、丙两种水果共22吨到A地销售,问装运乙、丙两种水果的汽车各多少辆?
(2)水果基地计划用20辆汽车装运甲、乙、丙三种水果共72吨到B地销售(每种水果不少于一车),假设装运甲水果的汽车为m辆,则装运乙、丙两种水果的汽车各多少辆?(结果用m表示)
(3)在(2)问的基础上,如何安排装运可使水果基地获得最大利润?最大利润是多少?
| 甲 | 乙 | 丙 | |
| 每辆汽车能装的数量(吨) | 4 | 2 | 3 |
| 每吨水果可获利润(千元) | 5 | 7 | 4 |
(2)水果基地计划用20辆汽车装运甲、乙、丙三种水果共72吨到B地销售(每种水果不少于一车),假设装运甲水果的汽车为m辆,则装运乙、丙两种水果的汽车各多少辆?(结果用m表示)
(3)在(2)问的基础上,如何安排装运可使水果基地获得最大利润?最大利润是多少?
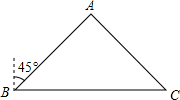 某物流公司派送人员甲、乙分别从B地派送货物到A、C两地,如图,A在B的北偏东45°方向,C在B的正东方向且BC=120km.乙的速度是60km/h,甲的速度是乙速度的$\sqrt{2}$倍,甲把货物送到A地后又接到A地一批货物要送到C地,结果两人同时到达C地.
某物流公司派送人员甲、乙分别从B地派送货物到A、C两地,如图,A在B的北偏东45°方向,C在B的正东方向且BC=120km.乙的速度是60km/h,甲的速度是乙速度的$\sqrt{2}$倍,甲把货物送到A地后又接到A地一批货物要送到C地,结果两人同时到达C地.