题目内容
 有一水库大坝的横截面是梯形ABCD,AD∥BC,EF为水库的水面,点E在DC上,某课题小组在老师的带领下想测量水的深度,他们测得背水坡AB的长为12米,迎水坡上DE的长为2米,∠BAD=135°,∠ADC=120°.
有一水库大坝的横截面是梯形ABCD,AD∥BC,EF为水库的水面,点E在DC上,某课题小组在老师的带领下想测量水的深度,他们测得背水坡AB的长为12米,迎水坡上DE的长为2米,∠BAD=135°,∠ADC=120°.(1)求大坝的高度;
(2)求水深.
考点:解直角三角形的应用-坡度坡角问题
专题:
分析:(1)分别过A、D作AM⊥BC于M,DG⊥BC于G.利用AB的长为12,∠BAD=135°可求得大坝的高度;
(2)根据这两条高相等,再利用DE长构造一直角三角形,求得DE的垂直距离,进而求得水深.
(2)根据这两条高相等,再利用DE长构造一直角三角形,求得DE的垂直距离,进而求得水深.
解答:解:(1)分别作AM⊥BC于M,DG⊥BC于G.过E作EH⊥DG于H,则四边形AMGD为矩形.
∵AD∥BC,∠BAD=135°,∠ADC=120°.
∴∠B=45°,∠DCG=60°,∠GDC=30°.
在Rt△ABM中,
AM=AB•sinB=12×
=6
(米);
(2)由(1)得,DG=6
.
在Rt△DHE中,
DH=DE•cos∠EDH=2×
=
,
∴HG=DG-DH=6
-
.
答:水深约为(6
-
)米.
∵AD∥BC,∠BAD=135°,∠ADC=120°.
∴∠B=45°,∠DCG=60°,∠GDC=30°.
在Rt△ABM中,

AM=AB•sinB=12×
| ||
| 2 |
| 2 |
(2)由(1)得,DG=6
| 2 |
在Rt△DHE中,
DH=DE•cos∠EDH=2×
| ||
| 2 |
| 3 |
∴HG=DG-DH=6
| 2 |
| 3 |
答:水深约为(6
| 2 |
| 3 |
点评:本题主要考查三角函数及解直角三角形的有关知识.解决本题的难点是作出辅助线构造直角三角形,是常作的辅助线.

练习册系列答案
 课课练江苏系列答案
课课练江苏系列答案 名牌中学课时作业系列答案
名牌中学课时作业系列答案 明天教育课时特训系列答案
明天教育课时特训系列答案 浙江新课程三维目标测评课时特训系列答案
浙江新课程三维目标测评课时特训系列答案
相关题目
下列语句,不是命题的是( )
| A、两点之间线段最短 |
| B、两直线不平行就相交 |
| C、连接A、B两点 |
| D、对顶角相等 |
 如图,OC是∠AOB的平分线,∠AOB=61°30′,求与∠AOC互补的角的大小.
如图,OC是∠AOB的平分线,∠AOB=61°30′,求与∠AOC互补的角的大小. 已知AD⊥BC,EF⊥BC,∠1=∠F.求证:AD平分∠BAC.
已知AD⊥BC,EF⊥BC,∠1=∠F.求证:AD平分∠BAC.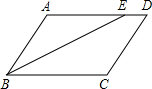 在?ABCD中,AB=6cm,AD=8cm,BE平分∠ABC,求DE的长度.
在?ABCD中,AB=6cm,AD=8cm,BE平分∠ABC,求DE的长度.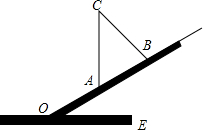 如图,一个坡度为1:
如图,一个坡度为1: