题目内容
8.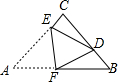 如图,在△ABC中,∠ACB=90°,AC=BC=4,将△ABC折叠,使点A落在BC边上的点D处,EF为折痕,若AE=3,则sin∠BFD的值为( )
如图,在△ABC中,∠ACB=90°,AC=BC=4,将△ABC折叠,使点A落在BC边上的点D处,EF为折痕,若AE=3,则sin∠BFD的值为( )| A. | $\frac{1}{3}$ | B. | $\frac{2\sqrt{2}}{3}$ | C. | $\frac{\sqrt{2}}{4}$ | D. | $\frac{3}{5}$ |
分析 由题意得:△AEF≌△DEF,故∠EDF=∠A;由三角形的内角和定理及平角的知识问题即可解决.
解答 解:∵在△ABC中,∠ACB=90°,AC=BC=4,
∴∠A=∠B,
由折叠的性质得到:△AEF≌△DEF,
∴∠EDF=∠A,
∴∠EDF=∠B,
∴∠CDE+∠BDF+∠EDF=∠BFD+∠BDF+∠B=180°,
∴∠CDE=∠BFD.
又∵AE=DE=3,
∴CE=4-3=1,
∴在直角△ECD中,sin∠CDE=$\frac{CE}{ED}$=$\frac{1}{3}$,
∴sin∠BFD=$\frac{1}{3}$.
故选:A.
点评 主要考查了翻折变换的性质及其应用问题;解题的关键是灵活运用全等三角形的性质、三角形的内角和定理等知识来解决问题.

练习册系列答案
相关题目
18.为纪念中国人民抗战战争的胜利,9月3日被确定为抗日战争胜利纪念日,某校为了了解学生对“抗日战争”的知晓情况,从全校6000名学生中,随机抽取了120名学生进行调查,在这次调查中( )
| A. | 6000名学生是总体 | |
| B. | 所抽取的每1名学生对“抗日战争”的知晓情况是总体的一个样本 | |
| C. | 120名是样本容量 | |
| D. | 所抽取的120名学生对“抗日战争”的知晓情况是总体的一个样本 |
16.5-1等于( )
| A. | 5 | B. | -$\frac{1}{5}$ | C. | -5 | D. | $\frac{1}{5}$ |
3.下列运算正确的是( )
| A. | 3a-a=0 | B. | a•a2=a3 | C. | a4÷a3=a2 | D. | (a3)2=a5 |
20.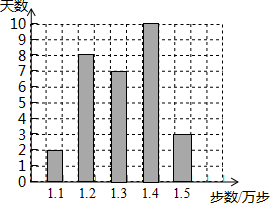 赵老师是一名健步走运动的爱好者,她用手机软件记录了某个月(30天)每天健步走的步数(单位:万步),将记录结果绘制成了如图所示的统计图.在每天所走的步数这组数据中,众数和中位数分别是( )
赵老师是一名健步走运动的爱好者,她用手机软件记录了某个月(30天)每天健步走的步数(单位:万步),将记录结果绘制成了如图所示的统计图.在每天所走的步数这组数据中,众数和中位数分别是( )
 赵老师是一名健步走运动的爱好者,她用手机软件记录了某个月(30天)每天健步走的步数(单位:万步),将记录结果绘制成了如图所示的统计图.在每天所走的步数这组数据中,众数和中位数分别是( )
赵老师是一名健步走运动的爱好者,她用手机软件记录了某个月(30天)每天健步走的步数(单位:万步),将记录结果绘制成了如图所示的统计图.在每天所走的步数这组数据中,众数和中位数分别是( )| A. | 1.2,1.3 | B. | 1.4,1.3 | C. | 1.4,1.35 | D. | 1.3,1.3 |