题目内容
8.把下列各数填在相应的位置:-5,+$\frac{1}{5}$,0.64,0,-1.1,$\frac{6}{7}$,8,|-10|,-(-5)(1)分数:+$\frac{1}{5}$,0.64,-1.1,$\frac{6}{7}$
(2)整数:-5,0,8,|-10|,-(-5)
(3)非负数:+$\frac{1}{5}$,0.64,0,$\frac{6}{7}$,8,|-10|,-(-5).
分析 先化简,再利用分数、整数和非负数的定义求解即可.
解答 解:|-10|=10,-(-5)=5,
(1)分数:+$\frac{1}{5}$,0.64,-1.1,$\frac{6}{7}$;
(2)整数:-5,0,8,|-10|,-(-5);
(3)非负数:+$\frac{1}{5}$,0.64,0,$\frac{6}{7}$,8,|-10|,-(-5).
故答案为:(1)+$\frac{1}{5}$,0.64,-1.1,$\frac{6}{7}$;(2)-5,0,8,|-10|,-(-5);(3)+$\frac{1}{5}$,0.64,0,$\frac{6}{7}$,8,|-10|,-(-5).
点评 本题主要考查了绝对值和有理数,解题的关键是利用分数、整数和非负数的定义求解.

练习册系列答案
 口算小状元口算速算天天练系列答案
口算小状元口算速算天天练系列答案
相关题目
8.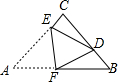 如图,在△ABC中,∠ACB=90°,AC=BC=4,将△ABC折叠,使点A落在BC边上的点D处,EF为折痕,若AE=3,则sin∠BFD的值为( )
如图,在△ABC中,∠ACB=90°,AC=BC=4,将△ABC折叠,使点A落在BC边上的点D处,EF为折痕,若AE=3,则sin∠BFD的值为( )
 如图,在△ABC中,∠ACB=90°,AC=BC=4,将△ABC折叠,使点A落在BC边上的点D处,EF为折痕,若AE=3,则sin∠BFD的值为( )
如图,在△ABC中,∠ACB=90°,AC=BC=4,将△ABC折叠,使点A落在BC边上的点D处,EF为折痕,若AE=3,则sin∠BFD的值为( )| A. | $\frac{1}{3}$ | B. | $\frac{2\sqrt{2}}{3}$ | C. | $\frac{\sqrt{2}}{4}$ | D. | $\frac{3}{5}$ |
16.若x轴上的一点P到y轴的距离为6,则点P的坐标为( )
| A. | (6,0) | B. | (6,0)或(-6,0) | C. | (0,6) | D. | (0,6)或(0,-6) |
20.已知关于x的方程ax2+bx+c=5的一个根是2,且二次函数y=ax2+bx+c的对称轴是直线x=2,则这条抛物线的顶点坐标为( )
| A. | (2,-3) | B. | (2,1) | C. | (2,5) | D. | (5,2) |