题目内容
13.先化简,再求值:$\frac{x+2}{x-2}$-$\frac{x-1}{x^2-4}$÷$\frac{1}{x+2}$,其中x=-1.分析 先把x2-4分解因式和除法运算化为乘法运算,再约分后进行同分母的减法运算得到原式=$\frac{3}{x-2}$,然后把x的值代入计算即可.
解答 解:原式=$\frac{x+2}{x-2}$-$\frac{x-1}{(x+2)(x-2)}$•(x+2)
=$\frac{x+2}{x-2}$-$\frac{x-1}{x-2}$
=$\frac{x+2-x+1}{x-2}$
=$\frac{3}{x-2}$,
当x=-1时,原式=$\frac{3}{-1-2}$=-1.
点评 本题考查了分式的化简求值:先把分式化简后,再把分式中未知数对应的值代入求出分式的值.在化简的过程中要注意运算顺序和分式的化简.化简的最后结果分子、分母要进行约分,注意运算的结果要化成最简分式或整式.

练习册系列答案
相关题目
3.关于x的一元二次方程kx2+4x+4=0有两个不相等的实数根,则k的取值范围是( )
| A. | k>-1 | B. | k>-1且k≠0 | C. | k<1 | D. | k<1且k≠0 |
1.已知点(-3,y1),(-2,y2)在反比例函数y=-$\frac{3}{x}$的图象上,则y1,y2的大小关系是( )
| A. | y1>y2 | B. | y1<y2 | C. | y1=y2 | D. | 无法确定 |
8.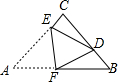 如图,在△ABC中,∠ACB=90°,AC=BC=4,将△ABC折叠,使点A落在BC边上的点D处,EF为折痕,若AE=3,则sin∠BFD的值为( )
如图,在△ABC中,∠ACB=90°,AC=BC=4,将△ABC折叠,使点A落在BC边上的点D处,EF为折痕,若AE=3,则sin∠BFD的值为( )
 如图,在△ABC中,∠ACB=90°,AC=BC=4,将△ABC折叠,使点A落在BC边上的点D处,EF为折痕,若AE=3,则sin∠BFD的值为( )
如图,在△ABC中,∠ACB=90°,AC=BC=4,将△ABC折叠,使点A落在BC边上的点D处,EF为折痕,若AE=3,则sin∠BFD的值为( )| A. | $\frac{1}{3}$ | B. | $\frac{2\sqrt{2}}{3}$ | C. | $\frac{\sqrt{2}}{4}$ | D. | $\frac{3}{5}$ |
18.下列计算正确的是( )
| A. | 2a•3a=6a | B. | (-a3)2=a6 | C. | 6a÷2a=3a | D. | (-2a)3=-6a3 |
12.边长为7,24,25的△ABC内有一点P到三边的距离相等,则这个距离是( )
| A. | 1 | B. | 3 | C. | 4 | D. | 6 |