题目内容
2.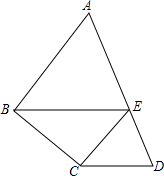 如图,在四边形ABCD中,E是AD边上的一点,EC∥AB,EB∥DC.
如图,在四边形ABCD中,E是AD边上的一点,EC∥AB,EB∥DC.(1)△ABE与△ECD相似吗?为什么?
(2)若△ABE的面积为3,△CDE的面积为1,求△BCE的面积.
分析 (1)由EC∥AB,EB∥DC,可得∠A=∠CED,∠AEB=∠D,即可证得△ABE与△ECD相似;
(2)由△ABE的面积为3,△CDE的面积为1,可得BE:CD=$\sqrt{3}$:1,又由EB∥CD,可得△BCE与△CDE等高,然后由等高三角形的面积比等于对应底的比,求得△BCE的面积.
解答 解:(1)相似.
理由:∵EC∥AB,EB∥DC,
∴∠A=∠CED,∠AEB=∠D,
∴△ABE∽△ECD;
(2)∵△ABE∽△CDE,且△ABE的面积为3,△CDE的面积为1,
∴BE:CD=$\sqrt{3}$:1,
∵EB∥CD,
∴△BCE与△CDE等高,
∴S△BCE:S△CDE=BE:CD=$\sqrt{3}$:1,
∴S△BCE=$\sqrt{3}$.
点评 此题考查了相似三角形的判定与性质.注意相似三角形的面积比等于相似比的平方、等高三角形面积的比等于其对应底的比.

练习册系列答案
 名校课堂系列答案
名校课堂系列答案
相关题目
12.为了提高节能意识,深圳某中学对全校的耗电情况进行了统计,他们抽查了10天中全校每天的耗电量,数据如下表:(单位:度)
(1)写出学校这10天耗电量的众数和平均数;
(2)若每度电的定价是0.8元,由上题获得的数据,估计该校每月应付电费是多少?(每月按30天计)
(3)如果做到人走电关,学校每天就可节省电量1%,按照每度电0.8元计算,写出该校节省电费y(元)与天数x(取正整数)之间的函数关系式.
| 度数 | 900 | 920 | 950 | 1010 | 1050 | 1100 |
| 天数 | 1 | 1 | 2 | 3 | 1 | 2 |
(2)若每度电的定价是0.8元,由上题获得的数据,估计该校每月应付电费是多少?(每月按30天计)
(3)如果做到人走电关,学校每天就可节省电量1%,按照每度电0.8元计算,写出该校节省电费y(元)与天数x(取正整数)之间的函数关系式.
12.如表是某一天河南省8个城市的最高气温预报,则这8个市的最高气温的众数与中位数分别是( )
| 城市 | 郑州 | 洛阳 | 开封 | 安阳 | 新乡 | 焦作 | 南阳 | 商丘 |
| 最高气温(℃) | 16 | 11 | 17 | 13 | 11 | 13 | 9 | 11 |
| A. | 11,13 | B. | 11,12.5 | C. | 11,12 | D. | 13,12 |
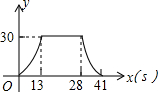
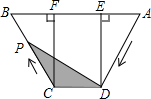 如图,梯形ABCD中,AB∥DC,DE⊥AB,CF⊥AB,垂足分别为E、F,且AE=EF=FB=5,DE=12,动点P从点C出发,沿C→B→A→D的方向以每秒1个单位长度的速度运动到点D停止,设运动时间为t秒,y=S△CDP,则y与t之间的函数图象大致是( )
如图,梯形ABCD中,AB∥DC,DE⊥AB,CF⊥AB,垂足分别为E、F,且AE=EF=FB=5,DE=12,动点P从点C出发,沿C→B→A→D的方向以每秒1个单位长度的速度运动到点D停止,设运动时间为t秒,y=S△CDP,则y与t之间的函数图象大致是( )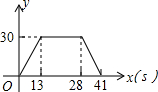
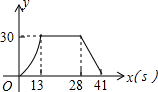

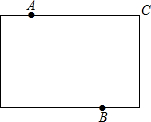 某地拟在新竣工的矩形广场的内部修建一个音乐喷泉,要求音乐喷泉P到广场的两个入口A、B的距离相等,且到广场管理处C的距离等于A和B之间距离的一半,A、B、C的位置如图所示.请利用尺规作图作出音乐喷泉P的位置.(要求:不写作法,但要保留作图痕迹,必须用铅笔作图).
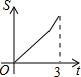
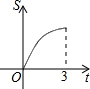
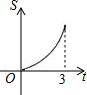
某地拟在新竣工的矩形广场的内部修建一个音乐喷泉,要求音乐喷泉P到广场的两个入口A、B的距离相等,且到广场管理处C的距离等于A和B之间距离的一半,A、B、C的位置如图所示.请利用尺规作图作出音乐喷泉P的位置.(要求:不写作法,但要保留作图痕迹,必须用铅笔作图).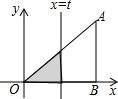 如图所示,直角三角形AOB中,AB⊥OB,且AB=OB=3.设直线l:x=t截此三角形所得的阴影部分面积为S,则S与t之间的函数关系的图象为(如选项所示)( )
如图所示,直角三角形AOB中,AB⊥OB,且AB=OB=3.设直线l:x=t截此三角形所得的阴影部分面积为S,则S与t之间的函数关系的图象为(如选项所示)( )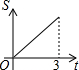
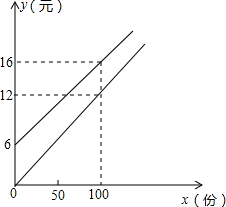 某校实施“学讲计划”教学,需印制若干份自主导学单,印刷厂有甲、乙两种收费方式,除按印数收取印刷费外,甲种方式还需收取制版费而乙种不需要,两种印刷方式的费用y(元)与印刷分数x(份)之间的函数关系如图所示:
某校实施“学讲计划”教学,需印制若干份自主导学单,印刷厂有甲、乙两种收费方式,除按印数收取印刷费外,甲种方式还需收取制版费而乙种不需要,两种印刷方式的费用y(元)与印刷分数x(份)之间的函数关系如图所示: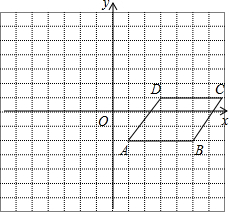 在直角坐标系中,平行四边形ABCD的位置如图.
在直角坐标系中,平行四边形ABCD的位置如图.