题目内容
14.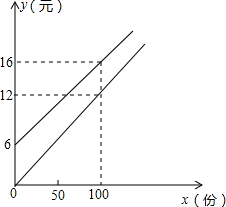 某校实施“学讲计划”教学,需印制若干份自主导学单,印刷厂有甲、乙两种收费方式,除按印数收取印刷费外,甲种方式还需收取制版费而乙种不需要,两种印刷方式的费用y(元)与印刷分数x(份)之间的函数关系如图所示:
某校实施“学讲计划”教学,需印制若干份自主导学单,印刷厂有甲、乙两种收费方式,除按印数收取印刷费外,甲种方式还需收取制版费而乙种不需要,两种印刷方式的费用y(元)与印刷分数x(份)之间的函数关系如图所示:(1)求甲、乙两种收费方式的函数关系式;
(2)该校九年级每次需印刷100-450(含100和450)份自主导学单,选择哪种收费方式较合算?
分析 (1)利用两函数图象上点的坐标,运用待定系数法分别求两函数解析式;
(2)通过比较两函数值得到当x<300,乙收费少;当x=300,甲乙收费一样;当x>300,甲收费少,于是对每次印刷100-450(含100和450)份自主导学单时,利用x的取值范围的变化确定选择收费方式.
解答 解:(1)设甲种收费方式的函数关系式为y=kx+b,
把(0,6),(100,16)分别代入得$\left\{\begin{array}{l}{b=6}\\{100k+b=16}\end{array}\right.$,解得$\left\{\begin{array}{l}{k=0.1}\\{b=6}\end{array}\right.$,
所以甲种收费方式的函数关系式为y=0.1x+6(x≥0),
设乙种收费方式的函数关系式为y=mx,
把(100,12)代入得100m=12,解得m=0.12,
所以乙种收费方式的函数关系式为y=0.12x(x≥0);
(2)当0.1x+6>0.12x时,解得x<300;
当0.1x+6=0.12x时,解得x=300,
当0.1x+6<0.12x时,解得x>300,
所以当100≤x<300时,选择乙种收费方式较合算;
当x=300时,两种收费方式一样;
当300≤x<450时,选择甲种收费方式较合算.
点评 本题考查了一次函数的应用:利用待定系数法求一次函数解析式,然后根据一次函数性质解决实际问题.注意自变量的取值范围.

练习册系列答案
 黄冈小状元解决问题天天练系列答案
黄冈小状元解决问题天天练系列答案 三点一测快乐周计划系列答案
三点一测快乐周计划系列答案
相关题目
3.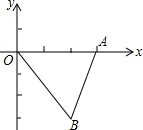 如图,平面直角坐标系中,点A、B的坐标分别为(3,0),(2,-3)若△AB′O′是△ABO关于点A的位似图形,且O′的坐标为(-1,0),则B′点的坐标为( )
如图,平面直角坐标系中,点A、B的坐标分别为(3,0),(2,-3)若△AB′O′是△ABO关于点A的位似图形,且O′的坐标为(-1,0),则B′点的坐标为( )
 如图,平面直角坐标系中,点A、B的坐标分别为(3,0),(2,-3)若△AB′O′是△ABO关于点A的位似图形,且O′的坐标为(-1,0),则B′点的坐标为( )
如图,平面直角坐标系中,点A、B的坐标分别为(3,0),(2,-3)若△AB′O′是△ABO关于点A的位似图形,且O′的坐标为(-1,0),则B′点的坐标为( )| A. | ($\frac{5}{3}$,-4) | B. | ($\frac{4}{3}$,-4) | C. | ($\frac{5}{3}$,4) | D. | ($\frac{4}{3}$,4) |
4.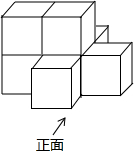 如图是一个由7个相同的小正方体搭成的几何体,这个几何体的主视图、左视图和俯视图中,是中心对称图形的是( )
如图是一个由7个相同的小正方体搭成的几何体,这个几何体的主视图、左视图和俯视图中,是中心对称图形的是( )
 如图是一个由7个相同的小正方体搭成的几何体,这个几何体的主视图、左视图和俯视图中,是中心对称图形的是( )
如图是一个由7个相同的小正方体搭成的几何体,这个几何体的主视图、左视图和俯视图中,是中心对称图形的是( )| A. | 主视图 | B. | 左视图 | C. | 俯视图 | D. | 左视图和俯视图 |
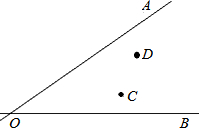 如图所示,107国道OA和320国道OB在某巿相交于O点,在∠AOB的内部有工厂C和D,现要建一个货站P,使P到OA和OB的距离相等,且使PC=PD,用尺规作出P点的位置.(不写作法,保留作图痕迹,写出结论)
如图所示,107国道OA和320国道OB在某巿相交于O点,在∠AOB的内部有工厂C和D,现要建一个货站P,使P到OA和OB的距离相等,且使PC=PD,用尺规作出P点的位置.(不写作法,保留作图痕迹,写出结论)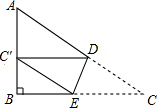 如图,△ABC中,∠B=90°,AB=6,BC=8,将△ABC沿DE折叠,使点C落在AB边的C′处,并且C′D∥BC,则CD的长是$\frac{40}{9}$.
如图,△ABC中,∠B=90°,AB=6,BC=8,将△ABC沿DE折叠,使点C落在AB边的C′处,并且C′D∥BC,则CD的长是$\frac{40}{9}$.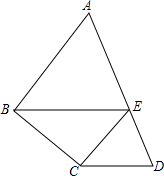 如图,在四边形ABCD中,E是AD边上的一点,EC∥AB,EB∥DC.
如图,在四边形ABCD中,E是AD边上的一点,EC∥AB,EB∥DC. 在如图的四边形MNOP中,证明:△PMO≌△NOM.
在如图的四边形MNOP中,证明:△PMO≌△NOM.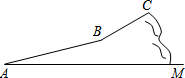 今年“五一”假期,某数学活动小组组织一次登山话动.他们从山脚下点A出发沿斜坡AB到达点B,再从点B沿斜坡BC到达山巅点C,路线如图所示. 斜坡AB的长为1 000米,斜坡BC的长为400米,在C点测得点B的俯角为30°.已知点A的海拔高度为121米,点C的海拔高度为921米.
今年“五一”假期,某数学活动小组组织一次登山话动.他们从山脚下点A出发沿斜坡AB到达点B,再从点B沿斜坡BC到达山巅点C,路线如图所示. 斜坡AB的长为1 000米,斜坡BC的长为400米,在C点测得点B的俯角为30°.已知点A的海拔高度为121米,点C的海拔高度为921米. 如图所示,已知2015是第k行的数字,则k等于673.
如图所示,已知2015是第k行的数字,则k等于673.