题目内容
8. 如图,AB、CD是⊙O的两条弦,AB⊥CD,垂足为点M,AM=4,BM=6,CM=3,DM=8,求⊙O的半径.
如图,AB、CD是⊙O的两条弦,AB⊥CD,垂足为点M,AM=4,BM=6,CM=3,DM=8,求⊙O的半径.
分析 分别作弦的弦心距,构造矩形,求出弦心距OE,连接OB,利用勾股定理,求出OB的长即可.
解答 解:作OE⊥AB于E,OF⊥CD于F,连接OB,如图所示: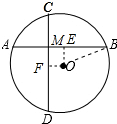
则CF=DF=$\frac{1}{2}$CD,AE=BE=$\frac{1}{2}$AB,
∵AM=4,BM=6,CM=3,DM=8
∴AB=10,CD=11,
∴CF=DF=5.5,AE=BE=5,
∴MF=5.5-3=2.5,
∵OE⊥AB,OF⊥CD,AB⊥CD,
∴四边形MEOF是矩形,
∴OE=MF=2.5,
在Rt△BOE中,OB=$\sqrt{B{E}^{2}+O{E}^{2}}$=$\sqrt{{5}^{2}+2.{5}^{2}}$=$\frac{5}{2}\sqrt{5}$,
即⊙O的半径为$\frac{5}{2}\sqrt{5}$.
点评 本题考查了垂径定理、矩形的判定与性质、勾股定理;熟练掌握垂径定理,由勾股定理求出OB是解决问题的关键.

练习册系列答案
相关题目
13.下列计算正确的是( )
| A. | (-p2q)3=-p5q3 | B. | 3m2÷(3m-1)=m-3m2 | ||
| C. | 15a2b3c÷($\frac{15}{2}$ab2)=2ab | D. | (x2-4x)x-1=x-4 |
 如图,在ABC中,∠A=∠B=30°,过点C作CD⊥AC,交AB于点D.
如图,在ABC中,∠A=∠B=30°,过点C作CD⊥AC,交AB于点D. 如图,在直线AD上任取一点O,过点O作射线OB,OE平分∠DOB,OC平分∠AOB,∠BOC=26°时,∠BOE的度数是64°.
如图,在直线AD上任取一点O,过点O作射线OB,OE平分∠DOB,OC平分∠AOB,∠BOC=26°时,∠BOE的度数是64°. 甲、乙二人从学校出发去科技馆,甲步行一段时间后,乙骑自行车沿相同路线行进,两人均匀速前行,他们的路程差s(米)与甲出发时间t(分)之间的函数关系如图所示.下列说法:①乙先到达青少年宫;②乙的速度是甲速度的2.5倍;③b=480;④a=24.其中正确的是①②③(填序号).
甲、乙二人从学校出发去科技馆,甲步行一段时间后,乙骑自行车沿相同路线行进,两人均匀速前行,他们的路程差s(米)与甲出发时间t(分)之间的函数关系如图所示.下列说法:①乙先到达青少年宫;②乙的速度是甲速度的2.5倍;③b=480;④a=24.其中正确的是①②③(填序号). 如图,在平面直角坐标系中,点A为双曲线y=$\frac{k}{x}$(x>0)上一点,以OA为一边向右作菱形OABC,且点C落在x轴正半轴上,边BC于双曲线交于点F,再以CF为一边向右作菱形CFED,点D也落在x轴正半轴上,连接AC、CE、AE,已知∠AOC=60°,S△ACE=$\sqrt{3}$,则S菱形OABC-S菱形CFED=2$\sqrt{3}$.
如图,在平面直角坐标系中,点A为双曲线y=$\frac{k}{x}$(x>0)上一点,以OA为一边向右作菱形OABC,且点C落在x轴正半轴上,边BC于双曲线交于点F,再以CF为一边向右作菱形CFED,点D也落在x轴正半轴上,连接AC、CE、AE,已知∠AOC=60°,S△ACE=$\sqrt{3}$,则S菱形OABC-S菱形CFED=2$\sqrt{3}$.