题目内容
20.已知方程组$\left\{\begin{array}{l}{2x+y=1+3m}\\{x+2y=5-m}\end{array}\right.$的解满足x-y>0,求m的取值范围.分析 先求出方程组的解,再解不等式求出m的取值范围即可.
解答 解:方程组$\left\{\begin{array}{l}{2x+y=1+3m}\\{x+2y=5-m}\end{array}\right.$的解为:$\left\{\begin{array}{l}{x=-1+\frac{7}{3}m}\\{y=3-\frac{5}{3}m}\end{array}\right.$
∵x-y>0,
∴-1+$\frac{7}{3}$m-3+$\frac{5}{3}m$>0,
∴m>1.
点评 本题考查了解二元一次方程组、一元一次不等式,解决本题的关键是解二元一次方程组.

练习册系列答案
相关题目
12.下列各式的乘积结果不含根式的是( )
| A. | 2$\sqrt{5}$×$\sqrt{5}$ | B. | 2$\sqrt{3}$×$3\sqrt{2}$ | C. | ($\sqrt{3}$+$\sqrt{2}$)×$[-(\sqrt{3}+\sqrt{2})]$ | D. | $\sqrt{3a-4b}•\sqrt{3a+4b}$ |
10. 如图,在正方形ABCD中,AB=2$\sqrt{2}$,连接AC,以点C为圆心、AC长为半径画弧,点E在BC的延长线上,则阴影部分的面积为( )
如图,在正方形ABCD中,AB=2$\sqrt{2}$,连接AC,以点C为圆心、AC长为半径画弧,点E在BC的延长线上,则阴影部分的面积为( )
 如图,在正方形ABCD中,AB=2$\sqrt{2}$,连接AC,以点C为圆心、AC长为半径画弧,点E在BC的延长线上,则阴影部分的面积为( )
如图,在正方形ABCD中,AB=2$\sqrt{2}$,连接AC,以点C为圆心、AC长为半径画弧,点E在BC的延长线上,则阴影部分的面积为( )| A. | 6π-4 | B. | 6π-8 | C. | 8π-4 | D. | 8π-8 |
 已知:如图,把菱形ABCD沿着AC方向平移得到菱形A1B1C1D1,BC与A1B1相交于点E,DC与A1D1相交于点F.求证:四边形A1ECF是菱形.
已知:如图,把菱形ABCD沿着AC方向平移得到菱形A1B1C1D1,BC与A1B1相交于点E,DC与A1D1相交于点F.求证:四边形A1ECF是菱形. 如图,AB、CD是⊙O的两条弦,AB⊥CD,垂足为点M,AM=4,BM=6,CM=3,DM=8,求⊙O的半径.
如图,AB、CD是⊙O的两条弦,AB⊥CD,垂足为点M,AM=4,BM=6,CM=3,DM=8,求⊙O的半径.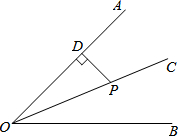 如图,OC是∠AOB的平分线,PD⊥DA,垂足为D,PD=2,则点P到OB的距离是2.
如图,OC是∠AOB的平分线,PD⊥DA,垂足为D,PD=2,则点P到OB的距离是2.