题目内容
17.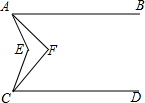 如图,已知AB∥CD,∠EAF$\frac{1}{4}$4∠EAB,∠ECF=$\frac{1}{4}$∠ECD,已知∠AEC=72°,则∠AFC=54°.
如图,已知AB∥CD,∠EAF$\frac{1}{4}$4∠EAB,∠ECF=$\frac{1}{4}$∠ECD,已知∠AEC=72°,则∠AFC=54°.
分析 连接AC,设∠EAF=x°,∠ECF=y°,∠EAB=4x°,∠ECD=4y°,根据平行线性质得出∠BAC+∠ACD=180°,求出∠CAE+∠ACE=180°-(4x°+4y°),求出∠AEC=4(x°+y°),∠AFC═3(x°+y°),即可得出答案.
解答 解: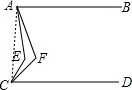
连接AC,设∠EAF=x°,∠ECF=y°,∠EAB=4x°,∠ECD=4y°,
∵AB∥CD,
∴∠BAC+∠ACD=180°,
∴∠CAE+4x°+∠ACE+4y°=180°,
∴∠CAE+∠ACE=180°-(4x°+4y°),∠FAC+∠FCA=180°-(3x°+3y°)
∴∠AEC=180°-(∠CAE+∠ACE)
=180°-[180°-(4x°+4y°)]
=4x°+4y°
=4(x°+y°),
∠AFC=180°-(∠FAC+∠FCA)
=180°-[180°-(3x°+3y°)]
=3x°+3y°
=3(x°+y°),
∴∠AFC=$\frac{3}{4}$∠AEC=$\frac{3}{4}$×72°=54°,
故答案为:54°.
点评 本题考查了平行线性质和三角形内角和定理的应用,注意:两直线平行,同旁内角互补.

练习册系列答案
 能考试期末冲刺卷系列答案
能考试期末冲刺卷系列答案
相关题目
7.先观察表格,再解决问题.
(1)1+2+3+4+5+…+40=820(直接写出结果);
(2)计算12+22+32+42+…+402的值;
(3)计算22+42+62+82+…+402的值.
| 项数 | 第一项 | 前两项 | 前三项 | 前四项 | 前五项 | |
| 式子① | 1 | 1+2 | 1+2+3 | 1+2+3+4 | 1+2+3+4+5 | |
| 式子② | 12 | 12+22 | 12+22+32 | 12+22+32+42 | 12+22+32+42+52 | |
| 两个式子的比 | 1 | $\frac{3}{5}$ | $\frac{3}{7}$ | $\frac{1}{3}$ | $\frac{3}{11}$ |
(2)计算12+22+32+42+…+402的值;
(3)计算22+42+62+82+…+402的值.
5. 如图,已知a∥b,且∠2是∠1的2倍,那么∠2的度数为( )
如图,已知a∥b,且∠2是∠1的2倍,那么∠2的度数为( )
 如图,已知a∥b,且∠2是∠1的2倍,那么∠2的度数为( )
如图,已知a∥b,且∠2是∠1的2倍,那么∠2的度数为( )| A. | 60° | B. | 90° | C. | 120° | D. | 150° |
6.对于二次函数 y=(x-1)2+2 的图象,下列说法正确的是( )
| A. | 开口向下 | B. | 顶点坐标是(-1,2) | ||
| C. | 对称轴是 x=1 | D. | 与 x 轴有两个交点 |
7.已知m是方程x2-x-2=0的一个根,则代数式m2-m+3=( )
| A. | -2 | B. | 1 | C. | 0 | D. | 5 |
 已知:⊙O上一点A,作⊙O的内接三角形ABC,使得△ABC为等边三角形.
已知:⊙O上一点A,作⊙O的内接三角形ABC,使得△ABC为等边三角形.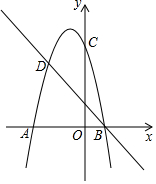 已知二次函数的图象与直线y=x+m交于x轴上一点A(-1,0),二次函数图象的顶点为C(1,-4).
已知二次函数的图象与直线y=x+m交于x轴上一点A(-1,0),二次函数图象的顶点为C(1,-4).