题目内容
2.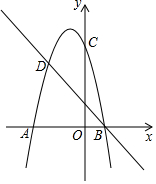 已知二次函数的图象与直线y=x+m交于x轴上一点A(-1,0),二次函数图象的顶点为C(1,-4).
已知二次函数的图象与直线y=x+m交于x轴上一点A(-1,0),二次函数图象的顶点为C(1,-4).(1)求这个二次函数的解析式;
(2)若二次函数的图象与x轴交于另一点B,与直线y=x+m交于另一点D,求
△ABD的面积.
分析 (1)设二次函数的解析式为y=a(x-1)2-4,把A(-1,0)代入求得a即可;
(2)令y=x2-2x-3=0,解方程可求得B点坐标,即可求得AB,把A(-1,0)代入y=x+m求得y=x+1,解方程组$\left\{\begin{array}{l}{y=x+1}\\{y={x}^{2}-2x-3}\end{array}\right.$求得D点坐标,根据三角形面积公式即可求得结论.
解答 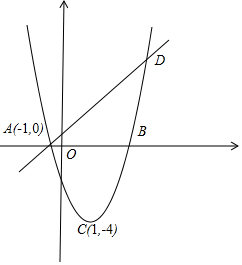 解:(1)如图,设二次函数的解析式为y=a(x-1)2-4,
解:(1)如图,设二次函数的解析式为y=a(x-1)2-4,
把A(-1,0)代入上式得:0=a(x-1)2-4,
解得:a=1,
∴这个二次函数的解析式为:y=(x-1)2-4,即y=x2-2x-3;
(2)令y=x2-2x-3=0,
解得:x1=-1,x2=3,
∴B(3,0),
把A(-1,0)代入y=x+m得:-1+m=0,
解得:m=1,
∴y=x+1,
解方程组$\left\{\begin{array}{l}{y=x+1}\\{y={x}^{2}-2x-3}\end{array}\right.$,
解得$\left\{\begin{array}{l}{{x}_{1}=-1}\\{{y}_{1}=0}\end{array}\right.$,$\left\{\begin{array}{l}{{x}_{2}=4}\\{{y}_{2}=5}\end{array}\right.$,
∴D(4,5),
∴AB=4,
∴△ABD的面积=$\frac{1}{2}$×4×5=10.
点评 本题主要考查了用顶点式求二次函数解析式,抛物线与坐标轴,直线的交点问题,三角形面积公式,熟知抛物线与坐标轴,直线的交点的求法是解题的关键.

练习册系列答案
 53随堂测系列答案
53随堂测系列答案
相关题目
7.某工厂大门是抛物线形水泥建筑物,大门宽为4m,顶部距地面的高度为4.4m,现有一辆满载货物的汽车欲通过大门,其装货宽度为2.4m,该车要想通过此门,装货后的最大高度应为( )
| A. | 2.80m | B. | 2.816m | C. | 2.82m | D. | 2.826m |
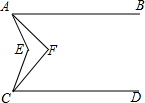 如图,已知AB∥CD,∠EAF$\frac{1}{4}$4∠EAB,∠ECF=$\frac{1}{4}$∠ECD,已知∠AEC=72°,则∠AFC=54°.
如图,已知AB∥CD,∠EAF$\frac{1}{4}$4∠EAB,∠ECF=$\frac{1}{4}$∠ECD,已知∠AEC=72°,则∠AFC=54°.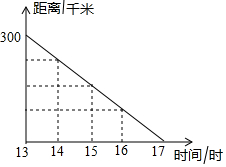 某客运汽车下午运行时距终点的距离与运行时间关系如图所示,13:00汽车距终点300千米,汽车于17时到达终点.
某客运汽车下午运行时距终点的距离与运行时间关系如图所示,13:00汽车距终点300千米,汽车于17时到达终点.