题目内容
20.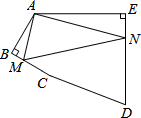 如图,在五边形ABCDE中,∠BAE=120°,∠B=∠E=90°,AB=BC=1,AE=DE=2,在BC,DE上分别找一点M,N,使△AMN的周长最小,则△AMN的最小周长为2$\sqrt{7}$.
如图,在五边形ABCDE中,∠BAE=120°,∠B=∠E=90°,AB=BC=1,AE=DE=2,在BC,DE上分别找一点M,N,使△AMN的周长最小,则△AMN的最小周长为2$\sqrt{7}$.
分析 根据要使△AMN的周长最小,即利用点的对称,让三角形的三边在同一直线上,作出A关于BC和ED的对称点A′,A″,连接A′A″即可得出最短路线,再利用勾股定理计算即可.
解答 解:作A关于BC和ED的对称点A′,A″,连接A′A″,交BC于M,交ED于N,则A′A″即为△AMN的周长最小值.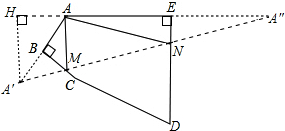
过点A′作EA延长线的垂线,垂足为H,
∵AB=BC=1,AE=DE=2,
∴AA′=2BA=2,AA″=2AE=4,
则Rt△A′HA中,∵∠EAB=120°,∴∠HAA′=60°,
∵A′H⊥HA,
∴∠AA′H=30°,
∴AH=$\frac{1}{2}$AA′=1,
∴A′H=$\sqrt{3}$,
A″H=1+4=5,
∴A′A″=$\sqrt{A′{H}^{2}+A′′{H}^{2}}$=2$\sqrt{7}$,
故答案为:2$\sqrt{7}$.
点评 本题主要考查了平面内最短路线问题求法以及勾股定理的应用,根据轴对称的性质得出M,N的位置是解题关键,注意轴对称的性质和勾股定理的正确运用.

练习册系列答案
 名校课堂系列答案
名校课堂系列答案
相关题目
10.若方程6kx-2y=8有一组解$\left\{\begin{array}{l}x=-3\\ y=2\end{array}$,则k的值等于( )
| A. | -$\frac{1}{6}$ | B. | $\frac{1}{6}$ | C. | $\frac{2}{3}$ | D. | -$\frac{2}{3}$ |
15.已知,反比例函数的图象经过点M(1,1)和N(-2,-$\frac{1}{2}$),则这个反比例函数是( )
| A. | y=$\frac{1}{x}$ | B. | y=-$\frac{1}{x}$ | C. | y=$\frac{2}{x}$ | D. | y=-$\frac{2}{x}$ |
9.已知两个数的和为正数,则( )
| A. | 一个加数为正,另一个加数为零 | |
| B. | 两个加数都为正数 | |
| C. | 两个加数一正一负,且正数的绝对值大于负数的绝对值 | |
| D. | 以上三种都有可能 |
 如图:∠A+∠B+∠C+∠D+∠E+∠F+∠G+∠H=360°.
如图:∠A+∠B+∠C+∠D+∠E+∠F+∠G+∠H=360°. 如图是小明制作的风筝,为了平衡制成了轴对称图形.已知OC所在的直线是对称轴,∠A=35°,∠BCO=30°,那么∠AOB=130°.
如图是小明制作的风筝,为了平衡制成了轴对称图形.已知OC所在的直线是对称轴,∠A=35°,∠BCO=30°,那么∠AOB=130°.