题目内容
13.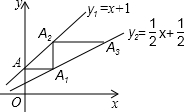 如图,直线y1=x+1交y轴于点A,过A作AA1∥x轴交直线y2=$\frac{1}{2}$x+$\frac{1}{2}$于点A1,过A1作A1A2∥y轴交直线y1于点A2,过A2作A2A3∥x轴交直线y2于点A3,…,按这个方式操作,则点A2013的坐标为(21006-1,21007).
如图,直线y1=x+1交y轴于点A,过A作AA1∥x轴交直线y2=$\frac{1}{2}$x+$\frac{1}{2}$于点A1,过A1作A1A2∥y轴交直线y1于点A2,过A2作A2A3∥x轴交直线y2于点A3,…,按这个方式操作,则点A2013的坐标为(21006-1,21007).
分析 先求出A,A1,A2,A3的坐标,找出规律,根据此规律即可得出结论.
解答 解:∵直线y1=x+1交y轴于点A,
∴A(0,1),
∵A作AA1∥x交直线y2=$\frac{1}{2}$x+$\frac{1}{2}$于点A1,
∴A1(1,1),
同理可得,A2(1,2),A3(3,2),A4(3,4),A5(7,4),A6(7,8),A7(15,8),
∴纵坐标为2,2,4,4,8,8,即第一组为21,…,第n组为2n,
∵$\frac{2013-2}{2}$=1005.5,
∴点A2013应该在1007组;
∴其纵坐标为21007,横坐标为21006-1.
故答案为:(21006-1,21007).
点评 本题考查的是一次函数图象上点的坐标特点,根据题意找出各点纵坐标的规律是解答此题的关键.

练习册系列答案
相关题目
3. 如图,△ABC≌△DCB,若∠A=75°,∠ACB=45°,则∠BCD等于( )
如图,△ABC≌△DCB,若∠A=75°,∠ACB=45°,则∠BCD等于( )
 如图,△ABC≌△DCB,若∠A=75°,∠ACB=45°,则∠BCD等于( )
如图,△ABC≌△DCB,若∠A=75°,∠ACB=45°,则∠BCD等于( )| A. | 80° | B. | 60° | C. | 40° | D. | 20° |
8.把多项式a4-4a2分解因式,结果正确的是( )
| A. | a2(a-4) | B. | a(a+2)(a-2) | C. | a2(a+2)(a-2) | D. | a2(a2-4) |
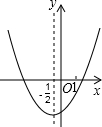 如图是二次函数y=ax2+bx+c(a≠0)的图象,对称轴为直线x=-$\frac{1}{2}$,下列结论:
如图是二次函数y=ax2+bx+c(a≠0)的图象,对称轴为直线x=-$\frac{1}{2}$,下列结论: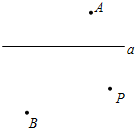 如图,平面上有直线a及直线a外的三点A、B、P.
如图,平面上有直线a及直线a外的三点A、B、P. 如图是二次函数y=ax2+bx+c(a≠0)图象的一部分,x=-1是对称轴,有下列判断:①b-2a=0;②4a-2b+c<0;③a-b+c=-9a;④若(-3,y1),($\frac{3}{2}$,y2)是抛物线上两点,则y1>y2,其中正确的序号是①③④.
如图是二次函数y=ax2+bx+c(a≠0)图象的一部分,x=-1是对称轴,有下列判断:①b-2a=0;②4a-2b+c<0;③a-b+c=-9a;④若(-3,y1),($\frac{3}{2}$,y2)是抛物线上两点,则y1>y2,其中正确的序号是①③④.