题目内容
1.下列命题正确的个数是( )①若代数式$\frac{\sqrt{2-2x}}{{x}^{2}-x}$有意义,则x的取值范围为x≤1,且x≠0
②若反比例函数y=$\frac{m}{x}$(m为常数),当x>0时,y随x增大而增大,则一次函数y=-2x+m的图象一定不经过第一象限
③H7N9禽流感病毒的直径大约为0.0000000805米,用科学记数法表示为8.05×10-9米
④数据2、5、7、2、3、3、6的中位数是3,众数是2
⑤点P(1,2)关于原点的对称点坐标为(-1,-2)
⑥“菱形的对角线互相垂直”的逆命题.
| A. | 1 | B. | 2 | C. | 3 | D. | 4 |
分析 根据分母不为0对①进行判断;根据反比例函数的性质得m<0,然后根据一次函数的性质对②进行判断;根据科学记数法的表示方法对③进行判断;根据众数的定义对④进行判断;根据关于原点对称的点的坐标特征对⑤进行判断;根据菱形的判定对⑥进行判断.
解答 解:若代数式$\frac{\sqrt{2-2x}}{{x}^{2}-x}$有意义,则x的取值范围为x≤1且x≠0,x≠-1,所以①错误;
若反比例函数y=$\frac{m}{x}$(m为常数),当x>0时,y随x增大而增大,所以m<0,所以一次函数y=-2x+m的图象一定不经过第一象限,所以②正确;
H7N9禽流感病毒的直径大约为0.0000000805米,用科学记数法表示为8.05×10-8米,所以③错误;
数据2、5、7、2、3、3、6的中位数是3,众数是2和3,所以④错误;
点P(1,2)关于原点的对称点坐标为(-1,-2),所以⑤正确;
“菱形的对角线互相垂直”的逆命题为对角线互相垂直的四边形为菱形,此逆命题错误.
故选B.
点评 本题考查了命题与定理:判断一件事情的语句,叫做命题.许多命题都是由题设和结论两部分组成,题设是已知事项,结论是由已知事项推出的事项,一个命题可以写成“如果…那么…”形式. 有些命题的正确性是用推理证实的,这样的真命题叫做定理.要说明一个命题的正确性,一般需要推理、论证,而判断一个命题是假命题,只需举出一个反例即可.

练习册系列答案
相关题目
11.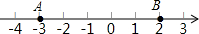 如图,数轴上的点A、B分别表示数-3、+2,若点C是AB的中点,则点C所表示的数是( )
如图,数轴上的点A、B分别表示数-3、+2,若点C是AB的中点,则点C所表示的数是( )
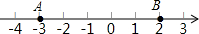 如图,数轴上的点A、B分别表示数-3、+2,若点C是AB的中点,则点C所表示的数是( )
如图,数轴上的点A、B分别表示数-3、+2,若点C是AB的中点,则点C所表示的数是( )| A. | 0 | B. | -$\frac{2}{3}$ | C. | -$\frac{1}{2}$ | D. | -1 |
9.一元二次方程x(x-4)=4-x的根是( )
| A. | -1 | B. | 4 | C. | 1和4 | D. | -1和4 |
6.点A(x1,y1),B(x2,y2),C(x3,y3)都在反比例函数y=$\frac{-2}{x}$的图象上,若x1<x2<0<x3,则y1,y2,y3的大小关系是( )
| A. | y2<y1<y3 | B. | y1<y2<y3 | C. | y3<y2<y1 | D. | y3<y1<y2 |
11. 如图,在?ABCD中,下列结论中一定正确的是( )
如图,在?ABCD中,下列结论中一定正确的是( )
 如图,在?ABCD中,下列结论中一定正确的是( )
如图,在?ABCD中,下列结论中一定正确的是( )| A. | AC⊥BD | B. | ∠A+∠D=180° | C. | AB=AD | D. | ∠A≠∠C |
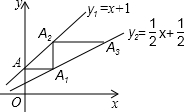 如图,直线y1=x+1交y轴于点A,过A作AA1∥x轴交直线y2=$\frac{1}{2}$x+$\frac{1}{2}$于点A1,过A1作A1A2∥y轴交直线y1于点A2,过A2作A2A3∥x轴交直线y2于点A3,…,按这个方式操作,则点A2013的坐标为(21006-1,21007).
如图,直线y1=x+1交y轴于点A,过A作AA1∥x轴交直线y2=$\frac{1}{2}$x+$\frac{1}{2}$于点A1,过A1作A1A2∥y轴交直线y1于点A2,过A2作A2A3∥x轴交直线y2于点A3,…,按这个方式操作,则点A2013的坐标为(21006-1,21007).