题目内容
4.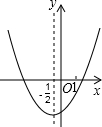 如图是二次函数y=ax2+bx+c(a≠0)的图象,对称轴为直线x=-$\frac{1}{2}$,下列结论:
如图是二次函数y=ax2+bx+c(a≠0)的图象,对称轴为直线x=-$\frac{1}{2}$,下列结论:①abc<0;②ax2+bx+c=0两根之和大于0;③a+b=0;④4a+c<2b;⑤b2-4ac>0;
正确的个数是( )
| A. | 1 | B. | 2 | C. | 3 | D. | 4 |
分析 由抛物线的开口方向判断a与0的关系,由抛物线与y轴的交点判断c与0的关系,然后根据对称轴及抛物线与x轴交点情况进行推理,进而对所得结论进行判断.
解答 解:①图象开口向上,a>0,与y轴交于负半轴,c<0,对称轴在y轴左侧,b>0,∴abc<0,①正确;
②∵对称轴为直线x=-$\frac{1}{2}$,∴-$\frac{{x}_{1}+{x}_{2}}{2}$=-$\frac{1}{2}$,x1+x2<0,②错误;
③∵a>0,b>0,∴a+b>0③错误;
④由图象和对称轴可知x=-2时,y<0,④正确;
⑤图象与x轴有2个交点,依据根的判别式可知b2-4ac>0,⑤正确.
故选:C.
点评 本题考查的是二次函数的图象与系数的关系,通过开口方向、对称轴、与坐标轴的交点确定系数和判别式的符号是解题的关键,解答时,注意数形结合思想的灵活运用.

练习册系列答案
相关题目
15.如图所示为魔术师在小丽面前表演的经过:

假设小丽所写数字为a,那么魔术师猜中的结果应为( )

假设小丽所写数字为a,那么魔术师猜中的结果应为( )
| A. | 2 | B. | 3 | C. | 4 | D. | a+4 |
9.一元二次方程x(x-4)=4-x的根是( )
| A. | -1 | B. | 4 | C. | 1和4 | D. | -1和4 |
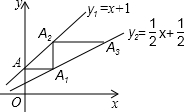 如图,直线y1=x+1交y轴于点A,过A作AA1∥x轴交直线y2=$\frac{1}{2}$x+$\frac{1}{2}$于点A1,过A1作A1A2∥y轴交直线y1于点A2,过A2作A2A3∥x轴交直线y2于点A3,…,按这个方式操作,则点A2013的坐标为(21006-1,21007).
如图,直线y1=x+1交y轴于点A,过A作AA1∥x轴交直线y2=$\frac{1}{2}$x+$\frac{1}{2}$于点A1,过A1作A1A2∥y轴交直线y1于点A2,过A2作A2A3∥x轴交直线y2于点A3,…,按这个方式操作,则点A2013的坐标为(21006-1,21007). 如图所示,把边长为1的正方形放在数轴上,以数1表示的点为圆心,正方形的对角线长为半径作弧,交数轴于点A,则点A表示的数是$1+\sqrt{2}$.
如图所示,把边长为1的正方形放在数轴上,以数1表示的点为圆心,正方形的对角线长为半径作弧,交数轴于点A,则点A表示的数是$1+\sqrt{2}$.