题目内容
2.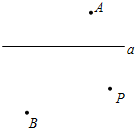 如图,平面上有直线a及直线a外的三点A、B、P.
如图,平面上有直线a及直线a外的三点A、B、P.(1)过点P画一条直线m,使得m∥a;
(2)若直线a、m表示一条河的两岸,现要在这条河上建一座桥(桥与岸垂直),使得从村庄A经桥过河到村庄B的路程最短,试问桥应建在何处?画出示意图.
分析 (1)把三角板的一条直角边与直线a重合,另一条直角边与直尺重合,然后把直尺三角板想P点平移,再过P点作直线即可.
(2)两点间直线距离最短,使BCMN为平行四边形即可,即BC垂直河岸且等于河宽,接连AC.
解答 解:(1)如图1所示,
(2)如图2,作AA'垂直于河岸a,使AA′等于河宽,
连接BA′,与另一条河岸相交于M,作MN⊥直线a,
则MN∥AA′且MN=AA′,
于是MNAA′为平行四边形,故MA′=NA.
根据“两点之间线段最短”,BA′最短,即AN+BM最短.
故桥建立在M、N处符合题意.
点评 此题考查了轴对称---最短路径问题,要利用“两点之间线段最短”,但许多实际问题没这么简单,需要我们将一些线段进行转化,即用与它相等的线段替代,从而转化成两点之间线段最短的问题.目前,往往利用对称性、平行四边形的相关知识进行转化.

练习册系列答案
相关题目
17.下列从左到右的变形是因式分解的是( )
| A. | (-a+b)2=a2-2ab+b2 | B. | m2-4m+3=(m-2)2-1 | ||
| C. | -a2+9b2=-(a+3b)(a-3b) | D. | (x-y)2=(x+y)2-4xy |
11. 如图,在?ABCD中,下列结论中一定正确的是( )
如图,在?ABCD中,下列结论中一定正确的是( )
 如图,在?ABCD中,下列结论中一定正确的是( )
如图,在?ABCD中,下列结论中一定正确的是( )| A. | AC⊥BD | B. | ∠A+∠D=180° | C. | AB=AD | D. | ∠A≠∠C |
12.南海是我国的固有领土,2014年在我国南海某海域探明可燃冰储量约有194亿立方米.194亿用科学记数法表示为( )
| A. | 1.94×109 | B. | 0.194×1010 | C. | 19.4×109 | D. | 1.94×1010 |
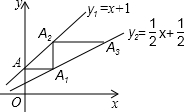 如图,直线y1=x+1交y轴于点A,过A作AA1∥x轴交直线y2=$\frac{1}{2}$x+$\frac{1}{2}$于点A1,过A1作A1A2∥y轴交直线y1于点A2,过A2作A2A3∥x轴交直线y2于点A3,…,按这个方式操作,则点A2013的坐标为(21006-1,21007).
如图,直线y1=x+1交y轴于点A,过A作AA1∥x轴交直线y2=$\frac{1}{2}$x+$\frac{1}{2}$于点A1,过A1作A1A2∥y轴交直线y1于点A2,过A2作A2A3∥x轴交直线y2于点A3,…,按这个方式操作,则点A2013的坐标为(21006-1,21007). 如图所示,把边长为1的正方形放在数轴上,以数1表示的点为圆心,正方形的对角线长为半径作弧,交数轴于点A,则点A表示的数是$1+\sqrt{2}$.
如图所示,把边长为1的正方形放在数轴上,以数1表示的点为圆心,正方形的对角线长为半径作弧,交数轴于点A,则点A表示的数是$1+\sqrt{2}$.