题目内容
9.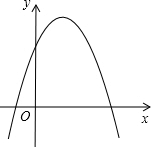 二次函数y=ax2+bx+c(a≠0)的图象如图所示,则:a<0;b>0;c>0;b2-4ac>0.
二次函数y=ax2+bx+c(a≠0)的图象如图所示,则:a<0;b>0;c>0;b2-4ac>0.
分析 由抛物线开口方向得到a<0,由抛物线对称轴为直线x=-$\frac{b}{2a}$得b>0;由抛物线与y轴的交点位置得c>0,根据抛物线与x轴的交点得出b2-4ac>0.
解答 解:∵抛物线开口向下,
∴a<0,
∵抛物线对称轴为直线x=-$\frac{b}{2a}$>0,
∴b>0;
∵抛物线与y轴的交点在x轴上方,
∴c>0,
∵抛物线与x轴的交点有两个,
∴b2-4ac>0.
故答案为:<;>;>;>.
点评 本题考查了二次函数图象与系数的关系:二次函数y=ax2+bx+c(a≠0),二次项系数a决定抛物线的开口方向和大小:当a>0时,抛物线向上开口;当a<0时,抛物线向下开口;一次项系数b和二次项系数a共同决定对称轴的位置:当a与b同号时(即ab>0),对称轴在y轴左; 当a与b异号时(即ab<0),对称轴在y轴右;常数项c决定抛物线与y轴交点:抛物线与y轴交于(0,c);抛物线与x轴交点个数:△=b2-4ac>0时,抛物线与x轴有2个交点;△=b2-4ac=0时,抛物线与x轴有1个交点;△=b2-4ac<0时,抛物线与x轴没有交点.

练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案
相关题目
19.在下列各组的条件中,不能判定△ABC和△DEF全等的是( )
| A. | AB=DE,∠B=∠E,∠C=∠F | B. | AC=DF,BC=DE,∠C=∠D | ||
| C. | AB=EF,∠A=∠E,∠B=∠F | D. | ∠A=∠F,∠B=∠E,AC=DE |
1.下列图案中既是轴对称图形又是中心对称图形的是( )
| A. |  | B. |  | C. |  | D. |  |
19.如果一个三角形两边的长分别等于一元二次方程x2-17x+66=0的两个实数根,那么这个三角形的周长可能是( )
| A. | 22 | B. | 23 | C. | 35 | D. | 36 |
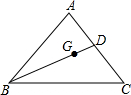 如图,BD是△ABC的中线,G为△ABC的重心,设$\overrightarrow{BA}$=$\overrightarrow{a}$,$\overrightarrow{BC}$=$\overrightarrow{b}$,试用$\overrightarrow{a}$,$\overrightarrow{b}$的线性组合表示向量$\overrightarrow{GB}$.
如图,BD是△ABC的中线,G为△ABC的重心,设$\overrightarrow{BA}$=$\overrightarrow{a}$,$\overrightarrow{BC}$=$\overrightarrow{b}$,试用$\overrightarrow{a}$,$\overrightarrow{b}$的线性组合表示向量$\overrightarrow{GB}$.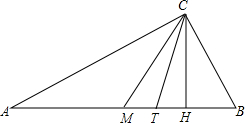 在△ABC中,M是AB中点,CH⊥AB于H,CT是∠ACB和∠MCH的平分线.求证:△ABC是直角三角形.
在△ABC中,M是AB中点,CH⊥AB于H,CT是∠ACB和∠MCH的平分线.求证:△ABC是直角三角形.