题目内容
13.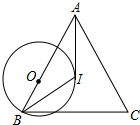 如图,在△ABC中,I是△ABC的内心,O是AB边上一点,⊙O经过B点且与AI相切于I点.若tan∠BAC=$\frac{24}{7}$,则sin∠C的值为( )
如图,在△ABC中,I是△ABC的内心,O是AB边上一点,⊙O经过B点且与AI相切于I点.若tan∠BAC=$\frac{24}{7}$,则sin∠C的值为( )| A. | $\frac{5}{6}$ | B. | $\frac{4}{5}$ | C. | $\frac{3}{5}$ | D. | $\frac{\sqrt{3}}{3}$ |
分析 延长AI交BC于D,连结OI,作BH⊥AC于H,如图,根据内心的性质得∠OBI=∠DBI,则可证明OI∥BD,再根据切线的性质得OI⊥AI,则BD⊥AD,加上AI平分∠BAC,所以△ABC为等腰三角形,得到AB=AC,接着在Rt△ABH中,利用正切的定义得到tan∠BAH=$\frac{BH}{AH}$=$\frac{24}{7}$,于是可设BH=24x,AH=7x,利用勾股定理得到AB=25x,则AC=AB=25x,CH=AC-AH=18x,然后在Rt△BCH中,利用勾股定理计算出BC=30x,再利用正弦的定义计算sinC的值.
解答 解:延长AI交BC于D,连结OI,作BH⊥AC于H,如图,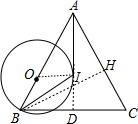
∵I是△ABC的内心,
∴BI平分∠ABC,即∠OBI=∠DBI,
∵OB=OI,
∴∠OBI=∠OIB,
∴∠DBI=∠OIB,
∴OI∥BD,
∵AI为⊙O的切线,
∴OI⊥AI,
∴BD⊥AD,
∵AI平分∠BAC,
∴△ABC为等腰三角形,
∴AB=AC,
在Rt△ABH中,tan∠BAH=$\frac{BH}{AH}$=$\frac{24}{7}$,
设BH=24x,AH=7x,
∴AB=$\sqrt{B{H}^{2}+A{H}^{2}}$=25x,
∴AC=AB=25x,
∴CH=AC-AH=25x-7x=18x,
在Rt△BCH中,BC=$\sqrt{C{H}^{2}+B{H}^{2}}$=30x,
∴sinC=$\frac{BH}{BC}$=$\frac{24x}{30x}$=$\frac{4}{5}$.
故选B.
点评 本题考查了三角形的内切圆与内心:与三角形各边都相切的圆叫三角形的内切圆,三角形的内切圆的圆心叫做三角形的内心,这个三角形叫做圆的外切三角形.三角形的内心就是三角形三个内角角平分线的交点.也考查了等腰三角形的判定与性质.

 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案| A. | x<5 | B. | x>5 | C. | x≥5 | D. | x≤5 |
| A. | (-3,-4) | B. | (2,4) | C. | (-3,9) | D. | (2,-1) |
| A. | 35° | B. | 145° | C. | 125° | D. | 55° |
| x/kg | 0 | 1 | 2 | 3 | 4 | 5 |
| y/cm | 10 | 10.5 | 11 | 11.5 | 12 | 12.5 |
| A. | x与y都是变量,且x是自变量,y是因变量 | |
| B. | 弹簧不挂重物时的长度为0 cm | |
| C. | 物体质量每增加1 kg,弹簧长度y增加0.5 cm | |
| D. | 所挂物体质量为7 kg时,弹簧长度为13.5 cm |
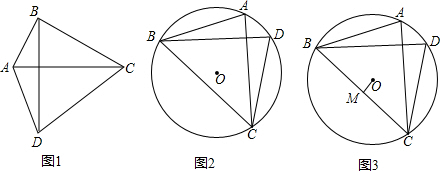
 如图,两条平行线AB、CD被直线BC所截,一组同旁内角的平分线相交于点E,则∠BEC的度数是90°.
如图,两条平行线AB、CD被直线BC所截,一组同旁内角的平分线相交于点E,则∠BEC的度数是90°. 如图,△ABC是等边三角形,若点A绕点C顺时针旋转30°至点A′,联结A′B,则∠ABA′度数是15°.
如图,△ABC是等边三角形,若点A绕点C顺时针旋转30°至点A′,联结A′B,则∠ABA′度数是15°. 如图,AB是⊙O的直径,C,D两点在⊙O上,∠BCD=25°,则∠AOD的度数为130°.
如图,AB是⊙O的直径,C,D两点在⊙O上,∠BCD=25°,则∠AOD的度数为130°.