题目内容
10.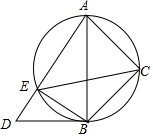 将一副三角板Rt△ABD与Rt△ACB(其中∠ABD=90°,∠D=60°,∠ACB=90°,∠ABC=45°)如图摆放,Rt△ABD中∠D所对直角边与Rt△ACB斜边恰好重合.以AB为直径的圆经过点C,且与AD交于点 E,分别连接EB,EC.
将一副三角板Rt△ABD与Rt△ACB(其中∠ABD=90°,∠D=60°,∠ACB=90°,∠ABC=45°)如图摆放,Rt△ABD中∠D所对直角边与Rt△ACB斜边恰好重合.以AB为直径的圆经过点C,且与AD交于点 E,分别连接EB,EC.(1)求证:EC平分∠AEB;
(2)求$\frac{{{S_{△{A}C{E}}}}}{{{S_{△{B}{E}C}}}}$的值.
分析 (1)由Rt△ACB中∠ABC=45°,得出∠BAC=∠ABC=45°,根据圆周角定理得出∠AEC=∠ABC,∠BEC=∠BAC,等量代换得出∠AEC=∠BEC,即EC平分∠AEB;
(2)方法1、设AB与CE交于点M.根据角平分线的性质得出$\frac{AM}{MB}$=$\frac{AE}{EB}$.易求∠BAD=30°,由直径所对的圆周角是直角得出∠AEB=90°,解直角△ABE得到AE=$\sqrt{3}$BE,那么$\frac{AM}{MB}$=$\frac{AE}{EB}$=$\sqrt{3}$.作AF⊥CE于F,BG⊥CE于G.证明△AFM∽△BGM,根据相似三角形对应边成比例得出$\frac{AF}{BG}$=$\frac{AM}{MB}$=$\sqrt{3}$,进而求出$\frac{{{S_{△{A}C{E}}}}}{{{S_{△{B}{E}C}}}}$=$\frac{\frac{1}{2}CE•AF}{\frac{1}{2}CE•BG}$=$\frac{AF}{BG}$=$\sqrt{3}$.
方法2、易求∠BAD=30°,由直径所对的圆周角是直角得出∠AEB=90°,解直角△ABE得到AE=$\sqrt{3}$BE,那么$\frac{AM}{MB}$=$\frac{AE}{EB}$=$\sqrt{3}$,再用角平分线定理判断出CP=CQ,即可得出结论.
解答 (1)证明:∵Rt△ACB中,∠ACB=90°,∠ABC=45°,
∴∠BAC=∠ABC=45°,
∵∠AEC=∠ABC,∠BEC=∠BAC,
∴∠AEC=∠BEC,
即EC平分∠AEB; (2)解:如图,设AB与CE交于点M.
(2)解:如图,设AB与CE交于点M.
∵EC平分∠AEB,
∴$\frac{AM}{MB}$=$\frac{AE}{EB}$.
在Rt△ABD中,∠ABD=90°,∠D=60°,
∴∠BAD=30°,
∵以AB为直径的圆经过点E,
∴∠AEB=90°,
∴tan∠BAE=$\frac{BE}{AE}$=$\frac{\sqrt{3}}{3}$,
∴AE=$\sqrt{3}$BE,
∴$\frac{AM}{MB}$=$\frac{AE}{EB}$=$\sqrt{3}$.
作AF⊥CE于F,BG⊥CE于G.
在△AFM与△BGM中,
∵∠AFM=∠BGM=90°,∠AMF=∠BMG,
∴△AFM∽△BGM,
∴$\frac{AF}{BG}$=$\frac{AM}{MB}$=$\sqrt{3}$,
∴$\frac{{{S_{△{A}C{E}}}}}{{{S_{△{B}{E}C}}}}$=$\frac{\frac{1}{2}CE•AF}{\frac{1}{2}CE•BG}$=$\frac{AF}{BG}$=$\sqrt{3}$.
方法2、如图1,
在Rt△ABD中,∠ABD=90°,∠D=60°,
∴∠BAD=30°,
∵以AB为直径的圆经过点E,
∴∠AEB=90°,
∴tan∠BAE=$\frac{BE}{AE}$=$\frac{\sqrt{3}}{3}$,
∴AE=$\sqrt{3}$BE,
过点C作CP⊥AE于P,过点C作CQ⊥EB交延长线于Q,
由(1)知,EC是∠AEB的角平分线,
∴CP=CQ,
∴$\frac{{{S_{△{A}C{E}}}}}{{{S_{△{B}{E}C}}}}$=$\frac{\frac{1}{2}AE•CP}{\frac{1}{2}BE•CQ}$=$\frac{AE}{BE}$=$\sqrt{3}$.
点评 本题考查了相似三角形的判定与性质,圆周角定理,锐角三角函数定义,通过作辅助线得出$\frac{AF}{BG}$=$\frac{AM}{MB}$=$\sqrt{3}$是解题的关键.

 津桥教育计算小状元系列答案
津桥教育计算小状元系列答案| A. | a=3cm,b=8cm,c=5cm | B. | a=12cm,b=5cm,c=6cm | ||
| C. | a=5cm,b=5cm,c=10cm | D. | a=15cm,b=10cm,c=7cm |
我们借助学习“图形的判定”获得的经验与方法对“平行四边形的判定”进一步探究.
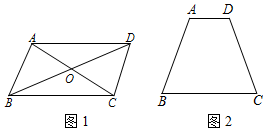
【初步思考】
在一个四边形中,我们把“一组对边平行、一组对边相等、一组对角相等或一条对角线被另一条对角线平分”称为一个条件.如图1,四边形ABCD中,我们用符号语言表示出所有的8个条件:
| ①AB=CD; | ②AD=BC; | ③AB∥CD; | ④AD∥BC; |
| ⑤∠BAD=∠BCD; | ⑥∠ABC=∠ADC; | ⑦OA=OC; | ⑧OB=OD. |
【深入探究】
小莉所在学习小组进行了研究,她们认为2个条件可分为以下六种类型:
Ⅰ关于对边的2个条件;Ⅱ关于对角的2个条件;
Ⅲ关于对角线的2个条件;Ⅳ关于边的条件与角的条件各1个;
Ⅴ关于边的条件与对角线的条件各1个;Ⅵ关于角的条件与对角线的条件各1个.
(1)小明认为“Ⅰ关于对边的2个条件”可分为“①②,③④,①③,①④”共4种不同种类的情形.请你仿照小明的叙述对其它五种类型进一步分类.
(2)小红认为有4种情形是平行四边形的判定依据.请你写出其它的三个判定定理.
定义:两组对边分别平行的四边形是平行四边形;
定理1:两组对边分别相等的四边形是平行四边形;
定理2:一组对边平行且相等的四边形是平行四边形;
定理3:对角线互相平分的四边形是平行四边形.
(3)小刚认为除了4个判定依据外,还存在一些真命题,他写出了其中的1个,请证明这个真命题,并仿照他的格式写出其它真命题(无需证明):
真命题1:四边形ABCD中,若∠BAD=∠BCD,∠ABC=∠ADC,则四边形ABCD是平行四边形.
(4)小亮认为,还存在一些假命题,他写出了其中的1个,并举反例进行了说明,请你仿照小亮的格式写出其它假命题并举反例进行说明.
假命题1:四边形ABCD中,若AB=CD,AD∥BC,则四边形ABCD不一定是平行四边形.
反例说明:如图2,四边形ABCD中,AB=CD,AD∥BC,显然四边形ABCD不是平行四边形.
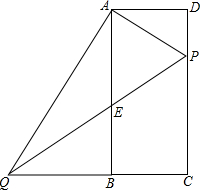 已知矩形ABCD中,AD=6,AB=12,P为边CD上的动点,过A点作AQ⊥AP,交CB的延长线于点Q,交AB于点E,若DP=x,CQ=y,
已知矩形ABCD中,AD=6,AB=12,P为边CD上的动点,过A点作AQ⊥AP,交CB的延长线于点Q,交AB于点E,若DP=x,CQ=y,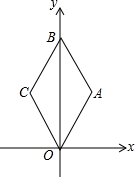 如图,在平面直角坐标系中,菱形OABC的边长为2,点B在y轴上,∠AOC=60°,则点B的坐标为(0,2$\sqrt{3}$).
如图,在平面直角坐标系中,菱形OABC的边长为2,点B在y轴上,∠AOC=60°,则点B的坐标为(0,2$\sqrt{3}$).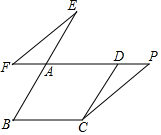 如图,在平行四边形ABCD中,延长BA至点E,使AE=AB,点F、P在边AD所在的直线上,EF∥CP.
如图,在平行四边形ABCD中,延长BA至点E,使AE=AB,点F、P在边AD所在的直线上,EF∥CP.