题目内容
16.在面积都相等的所有矩形中,当其中一个矩形的一边长为1时,它的另一边长为3.(1)设矩形的相邻两边长分别为x,y.
①求y关于x的函数表达式;
②当y≥3时,求x的取值范围;
(2)圆圆说其中有一个矩形的周长为6,方方说有一个矩形的周长为10,你认为圆圆和方方的说法对吗?为什么?
分析 (1)①直接利用矩形面积求法进而得出y与x之间的关系;②直接利用y≥3得出x的取值范围;
(2)直接利用x+y的值结合根的判别式得出答案.
解答 解:(1)①由题意可得:xy=3,
则y=$\frac{3}{x}$;
②当y≥3时,$\frac{3}{x}$≥3
解得:x≤1,
故x的取值范围是:0<x≤1;
(2)∵一个矩形的周长为6,
∴x+y=3,
∴x+$\frac{3}{x}$=3,
整理得:x2-3x+3=0,
∵b2-4ac=9-12=-3<0,
∴矩形的周长不可能是6;
所以圆圆的说法不对.
∵一个矩形的周长为10,
∴x+y=5,
∴x+$\frac{3}{x}$=5,
整理得:x2-5x+3=0,
∵b2-4ac=25-12=13>0,
∴矩形的周长可能是10,
所以方方的说法对.
点评 此题主要考查了反比例函数的应用以及一元二次方程的解法,正确得出y与x之间的关系是解题关键.

练习册系列答案
相关题目
12.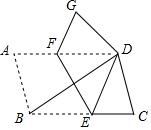 在?ABCD中,∠DBC=32°,现将?ABCD沿EF折叠,使点B与点D重合,点A落在G处,则∠GFE的度数( )
在?ABCD中,∠DBC=32°,现将?ABCD沿EF折叠,使点B与点D重合,点A落在G处,则∠GFE的度数( )
 在?ABCD中,∠DBC=32°,现将?ABCD沿EF折叠,使点B与点D重合,点A落在G处,则∠GFE的度数( )
在?ABCD中,∠DBC=32°,现将?ABCD沿EF折叠,使点B与点D重合,点A落在G处,则∠GFE的度数( )| A. | 132° | B. | 122° | C. | 112° | D. | 102° |
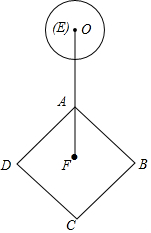 如图,边长为4cm的正方形ABCD,点F为正方形的中点,点E在FA的延长线上,EA=4cm,⊙O的半径为1cm,圆心O从点E出发向点F运动,小明发现:当EO满足①3<EO<5;②3≤EO≤5;③EO=4+$\sqrt{2}$;④EO=4+$3\sqrt{2}$时,⊙O与正方形ABCD的边只有两个公共点,你认为小明探究的结论中正确的有( )
如图,边长为4cm的正方形ABCD,点F为正方形的中点,点E在FA的延长线上,EA=4cm,⊙O的半径为1cm,圆心O从点E出发向点F运动,小明发现:当EO满足①3<EO<5;②3≤EO≤5;③EO=4+$\sqrt{2}$;④EO=4+$3\sqrt{2}$时,⊙O与正方形ABCD的边只有两个公共点,你认为小明探究的结论中正确的有( )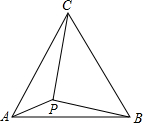 如图,△ABC为等边三角形,AB=2.若P为△ABC内一动点,且满足∠PAB=∠ACP,则线段PB长度的最小值为$\frac{2\sqrt{3}}{3}$.
如图,△ABC为等边三角形,AB=2.若P为△ABC内一动点,且满足∠PAB=∠ACP,则线段PB长度的最小值为$\frac{2\sqrt{3}}{3}$.
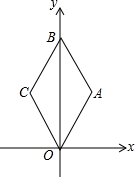 如图,在平面直角坐标系中,菱形OABC的边长为2,点B在y轴上,∠AOC=60°,则点B的坐标为(0,2$\sqrt{3}$).
如图,在平面直角坐标系中,菱形OABC的边长为2,点B在y轴上,∠AOC=60°,则点B的坐标为(0,2$\sqrt{3}$).