题目内容
16.设AB、CD是⊙O的两条弦,AB∥CD,若⊙O的半径为5,AB=8,CD=6,求AB与CD之间的距离.分析 由于弦AB、CD的具体位置不能确定,故应分两种情况进行讨论:①弦A和CD在圆心同侧;②弦A和CD在圆心异侧;作出半径和弦心距,利用勾股定理和垂径定理求解即可.
解答 解:①当弦AB和CD在圆心同侧时,如图①,
过点O作OF⊥CD,垂足为F,交AB于点E,连接OA,OC,
∵AB∥CD,
∴OE⊥AB,
∵AB=8,CD=6,
∴AE=4,CF=3,
∵OA=OC=5,
∴由勾股定理得:EO=$\sqrt{{5}^{2}-{4}^{2}}$=3,OF=$\sqrt{{5}^{2}-{3}^{2}}$=4,
∴EF=OF-OE=1;
②当弦AB和CD在圆心异侧时,如图②,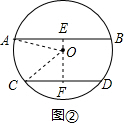
过点O作OE⊥AB于点E,反向延长OE交AD于点F,连接OA,OC,
EF=OF+OE=7,
所以AB与CD之间的距离是1或7.
点评 本题考查了勾股定理和垂径定理,解答此题时要注意进行分类讨论,不要漏解.

练习册系列答案
相关题目
4.已知关于x的方程-2x-b=0的解比关于x的方程$\frac{1}{3}$x+2b=0的解大-1,则b的值为( )
| A. | $\frac{2}{11}$ | B. | -$\frac{2}{11}$ | C. | x-1 | D. | -$\frac{4}{15}$ |
11.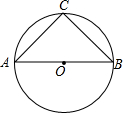 若等腰直角三角形的外接圆半径的长为2,则等腰直角三角形的直角边长为( )
若等腰直角三角形的外接圆半径的长为2,则等腰直角三角形的直角边长为( )
 若等腰直角三角形的外接圆半径的长为2,则等腰直角三角形的直角边长为( )
若等腰直角三角形的外接圆半径的长为2,则等腰直角三角形的直角边长为( )| A. | 2$\sqrt{2}$ | B. | 2$\sqrt{2}$-2 | C. | 2-$\sqrt{2}$ | D. | $\sqrt{2}$-1 |
8. 如图,AB=AC,下列条件不一定能证明△ABD≌△ACE的是( )
如图,AB=AC,下列条件不一定能证明△ABD≌△ACE的是( )
 如图,AB=AC,下列条件不一定能证明△ABD≌△ACE的是( )
如图,AB=AC,下列条件不一定能证明△ABD≌△ACE的是( )| A. | ∠B=∠C | B. | AE=AD | C. | BE=DC | D. | BD=CE |
5.下列各式中,正确的是( )
| A. | -4-2=-2 | B. | 10+(-8)=-2 | C. | 5-(-5)=0 | D. | -5-3-(-3)=-5 |
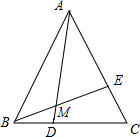 已知:如图,△ABC是等边三角形,点D、E分别在BC,AC且BD=CE,AD、BE相交于点M.求证:
已知:如图,△ABC是等边三角形,点D、E分别在BC,AC且BD=CE,AD、BE相交于点M.求证: