题目内容
12.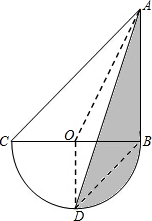 如图,三角形ABC是等腰直角三角形,D是圆周的中点,BC是半圆的直径,已知AB=BC=10厘米,那么阴影部分面积是多少?
如图,三角形ABC是等腰直角三角形,D是圆周的中点,BC是半圆的直径,已知AB=BC=10厘米,那么阴影部分面积是多少?
分析 根据题意得出OD∥AB,S△AOD=S△BOD,而S阴影=S△AOB+S扇形BOD-S△AOD,再根据面积公式计算即可.
解答 解:∵D是圆周的中点,BC是半圆的直径,
∴OD⊥BC,
∵∠ABC=90°,
∴OD∥AB,
∴S△AOD=S△BOD,
∴S阴影=S△AOB+S扇形BOD-S△AOD=S△AOB+S扇形BOD-S△BOD,
=$\frac{1}{2}$×10×10×$\frac{1}{2}$+$\frac{1}{4}π$×52-$\frac{1}{2}$×5×5
=25+$\frac{25}{4}$π-$\frac{25}{2}$
=$\frac{25}{2}$+$\frac{25}{4}$π,
答:阴影部分面积是$\frac{25}{2}$+$\frac{25}{4}$π.
点评 本题考查了勾股定理、等腰三角形的性质以及扇形和三角形的面积公式,解题的关键是利用等底等高等三角形的面积相等,把三角形AOD的面积转化为三角形BOD来解决问题.

练习册系列答案
相关题目
2.顺次连接正方形各边中点所得的四边形是( )
| A. | 等腰梯形 | B. | 正方形 | C. | 菱形 | D. | 矩形 |
20.已知一个正方形的面积是15,那么它的边长是( )
| A. | 15 | B. | $\sqrt{15}$ | C. | $\frac{1}{15}$ | D. | 以上皆不对 |
17.以Rt△ABC的两条直角边AB、BC为边,在三角形ABC的外部作等边三角形ABE和等边三角形BCF,EA和FC的延长线相交于点M,则点B一定是三角形EMF的( )
| A. | 垂心 | B. | 重心 | C. | 内心 | D. | 外心 |
2.在△ABC中,∠C=90°,AB=6,BC=4,则tanB的值是( )
| A. | $\frac{\sqrt{5}}{3}$ | B. | $\frac{2\sqrt{5}}{5}$ | C. | $\frac{2}{3}$ | D. | $\frac{\sqrt{5}}{2}$ |
 已知,如图,AD⊥BC,EF⊥BC,G为线段AB上的一个动点.
已知,如图,AD⊥BC,EF⊥BC,G为线段AB上的一个动点.