题目内容
 定义新运算:对于任意实数a,b,都有a⊕b=a(a-b)+1,等式右边是通常的加法、减法及乘法运算.比如:
定义新运算:对于任意实数a,b,都有a⊕b=a(a-b)+1,等式右边是通常的加法、减法及乘法运算.比如:2⊕5=2×(2-5)+1=2×(-3)+1=-6+1=-5.
若3⊕x的值小于13,求x的取位范围,并在图示的数轴上表示出来.
考点:解一元一次不等式,在数轴上表示不等式的解集
专题:新定义
分析:首先根据运算的定义,根据3⊕x的值小于13,即可列出关于x的不等式,解方程即可求解.
解答:解:∵3⊕x<13,
∴3(3-x)+1<13,
9-3x+1<13,
解得:x>-1.
 .
.
∴3(3-x)+1<13,
9-3x+1<13,
解得:x>-1.
 .
.点评:本题考查了不等式的性质:
(1)不等式的两边同时加上或减去同一个数或整式不等号的方向不变;
(2)不等式的两边同时乘以或除以同一个正数不等号的方向不变;
(3)不等式的两边同时乘以或除以同一个负数不等号的方向改变.
(1)不等式的两边同时加上或减去同一个数或整式不等号的方向不变;
(2)不等式的两边同时乘以或除以同一个正数不等号的方向不变;
(3)不等式的两边同时乘以或除以同一个负数不等号的方向改变.

练习册系列答案
 星级口算天天练系列答案
星级口算天天练系列答案 芒果教辅达标测试卷系列答案
芒果教辅达标测试卷系列答案
相关题目
 如图,AB是⊙O的直径,弦CD⊥AB,∠C=30°,CD=2
如图,AB是⊙O的直径,弦CD⊥AB,∠C=30°,CD=2| 3 |
| A、π | ||
| B、2π | ||
C、
| ||
| D、π |
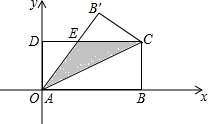 如图,在矩形ABCD中,AB=8,BC=4,将矩形沿AC折叠,点B落在B′处.
如图,在矩形ABCD中,AB=8,BC=4,将矩形沿AC折叠,点B落在B′处. 如图,在六边形ABCDEF中,AF∥CD,∠A=140°,∠C=165°.
如图,在六边形ABCDEF中,AF∥CD,∠A=140°,∠C=165°. 如图,在平行四边形ABCD中,E、F分别是对边BC和AD上的两点,且DF=BE.
如图,在平行四边形ABCD中,E、F分别是对边BC和AD上的两点,且DF=BE. 如图,已知直线AB经过⊙O上的点C,且OA=OB,CA=CB.
如图,已知直线AB经过⊙O上的点C,且OA=OB,CA=CB. 实数a、b、c在数轴上的对应点表示出来如图所示:请化简:
实数a、b、c在数轴上的对应点表示出来如图所示:请化简: 如图,A,B是边长为1的小正方形组成的网格的两个格点,在格点上任意放置点C.
如图,A,B是边长为1的小正方形组成的网格的两个格点,在格点上任意放置点C.