题目内容
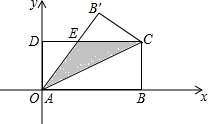 如图,在矩形ABCD中,AB=8,BC=4,将矩形沿AC折叠,点B落在B′处.
如图,在矩形ABCD中,AB=8,BC=4,将矩形沿AC折叠,点B落在B′处.(1)试判断图中△AEC的形状,并说明理由;
(2)求图中阴影部分的面积;
(3)求直线AB′所对应的函数解析式.
考点:翻折变换(折叠问题),待定系数法求一次函数解析式,矩形的性质
专题:计算题
分析:(1)根据矩形的性质得CD∥AB,再利用平行线的性质得∠BAC=∠DCA,然后根据折叠的性质得到∠BAC=∠B′AC,则∠DCA=∠B′AC,于是根据等腰三角形的判定定理可判断△AEC为等腰三角形;
(2)利用矩形的性质得CD=AB=8,AD=BC=4,设CE=x,则AE=x,DE=8-x,在Rt△ADE中,根据勾股定理得到42+(8-x)2=x2,解得x=5,然后根据三角形的面积公式计算图中阴影部分的面积;
(3)由于CE=5,则DE=3,可写出E点坐标为(3,4),然后利用待定系数法求直线AB′所对应的函数解析式.
(2)利用矩形的性质得CD=AB=8,AD=BC=4,设CE=x,则AE=x,DE=8-x,在Rt△ADE中,根据勾股定理得到42+(8-x)2=x2,解得x=5,然后根据三角形的面积公式计算图中阴影部分的面积;
(3)由于CE=5,则DE=3,可写出E点坐标为(3,4),然后利用待定系数法求直线AB′所对应的函数解析式.
解答:解:(1)△AEC为等腰三角形.理由如下:
∵四边形ABCD为矩形,
∵CD∥AB,
∴∠BAC=∠DCA,
∵矩形沿AC折叠,点B落在B′处,
∴∠BAC=∠B′AC,
∴∠DCA=∠B′AC,
∴△AEC为等腰三角形;
(2)∵四边形ABCD为矩形,
∴CD=AB=8,AD=BC=4,
设CE=x,则AE=x,DE=8-x,
在Rt△ADE中,
∵AD2+DE2=AE2,
∴42+(8-x)2=x2,解得x=5,
∴图中阴影部分的面积=
AD•CE=
×4×5=10;
(3)∵CE=5,
∴DE=3,
∴E点坐标为(3,4),
设直线AB′所对应的函数解析式为y=kx,
把E(3,4)代入得3k=4,解得k=
,
∴直线AB′所对应的函数解析式为y=
x.
∵四边形ABCD为矩形,
∵CD∥AB,
∴∠BAC=∠DCA,
∵矩形沿AC折叠,点B落在B′处,
∴∠BAC=∠B′AC,
∴∠DCA=∠B′AC,
∴△AEC为等腰三角形;
(2)∵四边形ABCD为矩形,
∴CD=AB=8,AD=BC=4,
设CE=x,则AE=x,DE=8-x,
在Rt△ADE中,
∵AD2+DE2=AE2,
∴42+(8-x)2=x2,解得x=5,
∴图中阴影部分的面积=
| 1 |
| 2 |
| 1 |
| 2 |
(3)∵CE=5,
∴DE=3,
∴E点坐标为(3,4),
设直线AB′所对应的函数解析式为y=kx,
把E(3,4)代入得3k=4,解得k=
| 4 |
| 3 |
∴直线AB′所对应的函数解析式为y=
| 4 |
| 3 |
点评:本题考查了折叠的性质:折叠是一种对称变换,它属于轴对称,折叠前后图形的形状和大小不变,位置变化,对应边和对应角相等.也考查了待定系数法求一次函数解析式和矩形的性质.

练习册系列答案
 小学学习好帮手系列答案
小学学习好帮手系列答案 小学同步三练核心密卷系列答案
小学同步三练核心密卷系列答案
相关题目
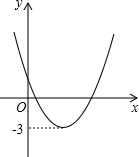 二次函数y=ax2+bx+c(a≠0)的图象如图,若ax2+bx+c=k有两个不相等的实数根,则k的取值范围是( )
二次函数y=ax2+bx+c(a≠0)的图象如图,若ax2+bx+c=k有两个不相等的实数根,则k的取值范围是( )| A、k>-3 | B、k<-3 |
| C、k=-3 | D、无法确定 |
下列命题中,假命题是( )
| A、梯形的两条对角线相等 |
| B、矩形的两条对角线相等 |
| C、菱形的两条对角线互相垂直 |
| D、正方形的每一条对角线平分一组对角 |
 如图,图象l1反映了某公司产品的销售收入y(单位:元)与销售量x(单位:吨)之间的关系,图象l2反映了该公司产品的产品成本y(元)与销售量x(吨)之间的关系,请根据图中所提供的信息解答下列问题:
如图,图象l1反映了某公司产品的销售收入y(单位:元)与销售量x(单位:吨)之间的关系,图象l2反映了该公司产品的产品成本y(元)与销售量x(吨)之间的关系,请根据图中所提供的信息解答下列问题: 如图,已知:ABCD是正方形,E是AD的中点.
如图,已知:ABCD是正方形,E是AD的中点. 已知:△ABC中,CD⊥AB,AC2=AD•AB,求证:CD2=AD•BD.
已知:△ABC中,CD⊥AB,AC2=AD•AB,求证:CD2=AD•BD. 定义新运算:对于任意实数a,b,都有a⊕b=a(a-b)+1,等式右边是通常的加法、减法及乘法运算.比如:
定义新运算:对于任意实数a,b,都有a⊕b=a(a-b)+1,等式右边是通常的加法、减法及乘法运算.比如: