题目内容
6.若抛物线L:y=ax2+bx+c(a,b,c是常数,a≠0)与直线l:y=ax+b满足a2+b2=2a(2c-b),则称此直线l与该抛物线L具有“支干”关系.此时,直线l叫做抛物线L的“支线”,抛物线L叫做直线l的“干线”.(1)若直线y=x-2与抛物线y=ax2+bx+c具有“支干”关系,求“干线”的最小值;
(2)若抛物线y=x2+bx+c的“支线”与y=-$\frac{4c}{x}$的图象只有一个交点,求反比例函数的解析式;
(3)已知“干线”y=ax2+bx+c与它的“支线”交于点P,与它的“支线”的平行线l′:y=ax+4a+b交于点A,B,记△ABP得面积为S,试问:$\frac{S}{|a|}$的值是否为定值?若是,请求出这个定值;若不是,请说明理由.
分析 (1)根据“支干”关系的定义,求出a、b、c的值,利用配方法确定函数的最值.
(2)由题意a=1,1+b2=2(2c-b) ①,可得抛物线y=x2+bx+c的“支线”为y=x+b,由$\left\{\begin{array}{l}{y=x+b}\\{y=-\frac{4c}{x}}\end{array}\right.$,消去y得到x2+bx+4c=0,由抛物线y=x2+bx+c的“支线”与y=-$\frac{4c}{x}$的图象只有一个交点,可知△=0,得b2-16c=0 ②,由①②解方程组即可解决问题.
(3)$\frac{S}{|a|}$的值是定值.不妨设a>0,如图所示,y=ax2+bx+c与它的“支线”交y轴于C,直线y=ax+4a+b与y轴交于点D,A(x1,y1),B(x2,y2),
由$\left\{\begin{array}{l}{y=a{x}^{2}+bx+c}\\{y=ax+4a+b}\end{array}\right.$,消去y得到ax2+(b-a)x+c-4a-b=0,推出x1+x2=$\frac{a-b}{a}$,x1x2=$\frac{c-4a-b}{a}$,推出|x1-x2|=$\sqrt{({x}_{1}+{x}_{2})^{2}-4{x}_{1}{x}_{2}}$=$\sqrt{(\frac{a-b}{a})^{2}-\frac{4(c-4a-b)}{a}}$=$\sqrt{\frac{{a}^{2}-2ab+{b}^{2}-4ac+16{a}^{2}+4ab}{{a}^{2}}}$,把a2+b2=2a(2c-b)代入上式化简得到|x1-x2|=4,由AB∥PC,可得S=S△PAB=S△CAB=S△CDB-S△CDA═$\frac{1}{2}$•CD•|Bx-Ax|=$\frac{1}{2}$•|4a|•4=8•|a|,由此即可解决问题.
解答 解:(1)由题意a=1,b=-2,12+(-2)2=2(2c+2),解得c=$\frac{1}{4}$,
∴抛物线的解析式为y=x2-2x+$\frac{1}{4}$,
∵y=x2-2x+$\frac{1}{4}$=(x-1)2-$\frac{3}{4}$,
∵a=1>0,
∴x=1时,y有最小值,最小值为-$\frac{3}{4}$.
(2)由题意a=1,1+b2=2(2c-b) ①
∴抛物线y=x2+bx+c的“支线”为y=x+b,
由$\left\{\begin{array}{l}{y=x+b}\\{y=-\frac{4c}{x}}\end{array}\right.$,消去y得到x2+bx+4c=0,
∵抛物线y=x2+bx+c的“支线”与y=-$\frac{4c}{x}$的图象只有一个交点,
∴△=0,
∴b2-16c=0 ②
由①②可得b=-2,c=$\frac{1}{4}$或b=-$\frac{2}{3}$,c=$\frac{1}{36}$,
∴反比例函数的解析式为y=-$\frac{1}{x}$或y=-$\frac{1}{9x}$.
(3)$\frac{S}{|a|}$的值是定值.理由如下:
不妨设a>0,如图所示,y=ax2+bx+c与它的“支线”交y轴于C,直线y=ax+4a+b与y轴交于点D,A(x1,y1),B(x2,y2),
由$\left\{\begin{array}{l}{y=a{x}^{2}+bx+c}\\{y=ax+4a+b}\end{array}\right.$,消去y得到ax2+(b-a)x+c-4a-b=0,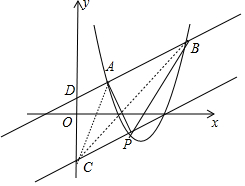
∴x1+x2=$\frac{a-b}{a}$,x1x2=$\frac{c-4a-b}{a}$,
∴|x1-x2|=$\sqrt{({x}_{1}+{x}_{2})^{2}-4{x}_{1}{x}_{2}}$=$\sqrt{(\frac{a-b}{a})^{2}-\frac{4(c-4a-b)}{a}}$=$\sqrt{\frac{{a}^{2}-2ab+{b}^{2}-4ac+16{a}^{2}+4ab}{{a}^{2}}}$,
把a2+b2=2a(2c-b)代入上式化简得到|x1-x2|=4,
∵AB∥PC,
∴S=S△PAB=S△CAB=S△CDB-S△CDA═$\frac{1}{2}$•CD•|Bx-Ax|=$\frac{1}{2}$•|4a|•4=8•|a|,
∴$\frac{S}{|a|}$=8,$\frac{S}{|a|}$的值是定值.
点评 本题考查二次函数综合题、一次函数的应用、反比例函数的性质、一元二次方程的根与系数关系等知识,解题的关键是理解题意,学会构建方程组解决问题,学会用分割法求三角形的面积,学会利用参数解决问题,属于中考压轴题.

 全优点练单元计划系列答案
全优点练单元计划系列答案| A. | 有两个相等的实数根 | B. | 有两个不相等的实数根 | ||
| C. | 无实数根 | D. | 有一根为0 |
| A. | y=x2-16x+55 | B. | y=x2+8x+7 | C. | y=-x2+8x+7 | D. | y=x2-8x+7 |
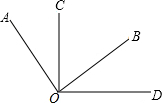 如图,∠AOB=∠COD=90°
如图,∠AOB=∠COD=90°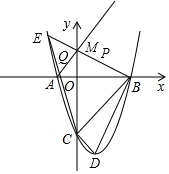 如图,抛物线y=x2+2ax+3a与x轴交于点A,B(点A在点B左侧),与y轴的负半轴交于点C,顶点为D,且OB=OC.
如图,抛物线y=x2+2ax+3a与x轴交于点A,B(点A在点B左侧),与y轴的负半轴交于点C,顶点为D,且OB=OC.