题目内容
15.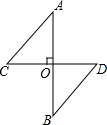 如图,AB⊥CD于O,且AO=BO,根据提示,添加一个条件使得Rt△AOC≌Rt△BOD.
如图,AB⊥CD于O,且AO=BO,根据提示,添加一个条件使得Rt△AOC≌Rt△BOD.(1)OC=OD(SAS) (2)AC=BD(HL)
(3)∠C=∠D(AAS) (4)∠A=∠B(ASA)
分析 (1)条件为OD=OC,根据SAS推出即可;
(2)条件为AC=BD,根据HL推出即可;
(3)条件为∠C=∠D,根据AAS推出即可;
(4)条件为∠A=∠B,根据ASA推出即可.
解答 解:(1)OC=OD,
理由是:在△AOC和△BOD中,
$\left\{\begin{array}{l}{OA=OB}\\{∠AOC=∠BOD}\\{OC=OD}\end{array}\right.$,
∴△AOC≌△BOD(SAS).
故答案为:OC=OD;
(2)AC=BD,
理由是:∵AB⊥CD,
∴∠AOC=∠BOD=90°,
在Rt△AOC和Rt△BOD中,
$\left\{\begin{array}{l}{AC=BD}\\{OA=OB}\end{array}\right.$,
∴Rt△AOC≌Rt△BOD(HL).
故答案为:AC=BD;
(3)∠C=∠D,
理由是:在△AOC和△BOD中,
$\left\{\begin{array}{l}{∠AOC=∠BOD}\\{∠C=∠D}\\{OA=OB}\end{array}\right.$,
∴△AOC≌△BOD(AAS).
故答案为:∠C=∠D;
(4)∠A=∠B,
理由是:在△AOC和△BOD中,
$\left\{\begin{array}{l}{∠A=∠B}\\{AO=OB}\\{∠AOC=∠BOD}\end{array}\right.$,
∴△AOC≌△BOD(ASA).
故答案为:∠A=∠B.
点评 此题主要考查了全等三角形的判定的应用,关键是找出能使三角形全等的条件,注意:全等三角形的判定定理有SAS,ASA,AAS,SSS.

练习册系列答案
相关题目
10.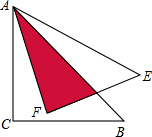 如图,将等腰直角三角形ABC绕点A逆时针旋转15度得到△AEF,若AC=$\sqrt{3}$,则阴影部分的面积为( )
如图,将等腰直角三角形ABC绕点A逆时针旋转15度得到△AEF,若AC=$\sqrt{3}$,则阴影部分的面积为( )
 如图,将等腰直角三角形ABC绕点A逆时针旋转15度得到△AEF,若AC=$\sqrt{3}$,则阴影部分的面积为( )
如图,将等腰直角三角形ABC绕点A逆时针旋转15度得到△AEF,若AC=$\sqrt{3}$,则阴影部分的面积为( )| A. | 1 | B. | $\frac{1}{2}$ | C. | $\frac{{\sqrt{3}}}{2}$ | D. | $\sqrt{3}$ |
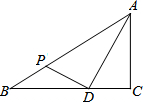 如图,△ABC中,∠C=90°,AD平分∠BAC,BD=4cm,CD=3cm,点P是边AB上的动点,则DP长的最小值为3cm.
如图,△ABC中,∠C=90°,AD平分∠BAC,BD=4cm,CD=3cm,点P是边AB上的动点,则DP长的最小值为3cm.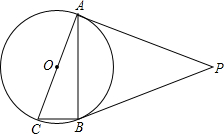 如图,⊙O是Rt△ABC的外接圆,∠ABC=90°,点P是圆外一点,PA切⊙O于点A,且PA=PB.
如图,⊙O是Rt△ABC的外接圆,∠ABC=90°,点P是圆外一点,PA切⊙O于点A,且PA=PB. 如图,将长方形纸片ABCD沿AE向上折叠,使点B落在DC边上的F点处,若△AFD的周长为9,△FCE的周长为3,则长方形ABCD的周长为12.
如图,将长方形纸片ABCD沿AE向上折叠,使点B落在DC边上的F点处,若△AFD的周长为9,△FCE的周长为3,则长方形ABCD的周长为12. 在学校开展的综合实践活动中,八年级某班对本班的40名学生进行了小制作评比,作品上交时间为5月1日至31日,评委把同学们上交作品的件数按5天一组分组统计,绘制了频数直方图(如图),图中从左到右依次为第一、二、三、四、五、六组.
在学校开展的综合实践活动中,八年级某班对本班的40名学生进行了小制作评比,作品上交时间为5月1日至31日,评委把同学们上交作品的件数按5天一组分组统计,绘制了频数直方图(如图),图中从左到右依次为第一、二、三、四、五、六组.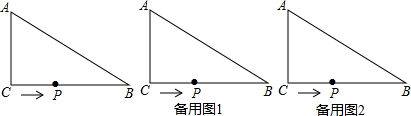
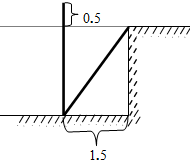 如图,小刚准备测量一条河的深度,他把一根竹竿垂直插到离岸边1.5米远的水底(不计淤泥深度),竹竿高出水面0.5米,再把竹竿的顶端拉向岸边,竿顶和岸边的水面刚好相齐;请推断河水的深度为几米?
如图,小刚准备测量一条河的深度,他把一根竹竿垂直插到离岸边1.5米远的水底(不计淤泥深度),竹竿高出水面0.5米,再把竹竿的顶端拉向岸边,竿顶和岸边的水面刚好相齐;请推断河水的深度为几米?