题目内容
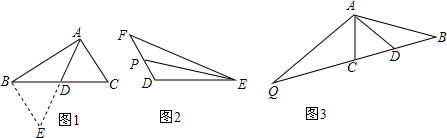
4.如图,在△ABC中,∠ACB=90°,AC=6cm,BC=8cm,动点P从点C出发,按C→B→A的路径,以2cm每秒的速度运动,设运动时间为t秒.
(1)当t=1时,求△ACP的面积.
(2)t为何值时,线段AP是∠CAB的平分线?
(3)请利用备用图2继续探索:当t为何值时,△ACP是以AC为腰的等腰三角形?(直接写出结论)
分析 (1)把t=1代入得出CP=2,利用三角形的面积进行解答即可;
(2)过P作PE⊥AB,设CP=2t,根据角平分线的性质和勾股定理进行解答即可;
(3)根据AC=CP,利用等腰直角三角形的性质解答即可.
解答 解:(1)把t=1得出CP=2,所以△ACP的面积=$\frac{1}{2}×2×6=6c{m}^{2}$;
(2)过P作PE⊥AB,如图1:
CP=2t,BP=(8-2t)cm,AE=AC=6cm,PE=CP=2t,BE=10-6=4,
可得:(8-2t)2=(2t)2-42
解得:t=$\frac{3}{2}s$;
(3)如图2,3,4:


因为△ACP是以AC为腰的等腰三角形,
当AC=CP=6时,t1=6÷2=3s;
当AC=CP=6时,${t}_{2}=4+\frac{7}{5}=\frac{27}{5}s$;
当AC=AP=6时,${t}_{3}=4+\frac{4}{2}=6$s.
点评 本题考查了等腰三角形的判定,三角形的面积,难度适中.利用分类讨论的思想是解(3)题的关键.

练习册系列答案
 全能测控一本好卷系列答案
全能测控一本好卷系列答案
相关题目
9.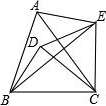 如图,△ABC和△EDC都是等边三角形,连接BD、AE、BE,∠DBE=20°,则∠AEB=( )
如图,△ABC和△EDC都是等边三角形,连接BD、AE、BE,∠DBE=20°,则∠AEB=( )
 如图,△ABC和△EDC都是等边三角形,连接BD、AE、BE,∠DBE=20°,则∠AEB=( )
如图,△ABC和△EDC都是等边三角形,连接BD、AE、BE,∠DBE=20°,则∠AEB=( )| A. | 30 | B. | 40 | C. | 45 | D. | 60 |
16.实际测量一座山的高度时,可在若干个观测点中测量每两个相邻可视观测点的相对高度,然后用这些相对高度计算出山的高度.下表是某次测量数据的部分记录(用A-C表示观测点A相对观测点C的高度)根据这次测量的数据:
则可得观测点A相对观测点B的高度是230米.
| A-C | C-D | E-D | E-F | G-F | B-G |
| 90m | 80m | 50 | -40m | -70m | 20m |
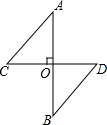 如图,AB⊥CD于O,且AO=BO,根据提示,添加一个条件使得Rt△AOC≌Rt△BOD.
如图,AB⊥CD于O,且AO=BO,根据提示,添加一个条件使得Rt△AOC≌Rt△BOD.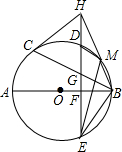 如图,AB、BC分别是⊙O的直径和弦,点D为$\widehat{BC}$上一点,弦DE交⊙O于点E,交AB于点F,交BC于点G,过点C的切线交ED的延长线于H,且HC=HG,连接BH,交⊙O于点M,连接MD、ME、BE.求证:
如图,AB、BC分别是⊙O的直径和弦,点D为$\widehat{BC}$上一点,弦DE交⊙O于点E,交AB于点F,交BC于点G,过点C的切线交ED的延长线于H,且HC=HG,连接BH,交⊙O于点M,连接MD、ME、BE.求证: