题目内容
10．
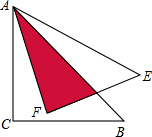如图，将等腰直角三角形ABC绕点A逆时针旋转15度得到△AEF，若AC=$\sqrt{3}$，则阴影部分的面积为（ ）| A． | 1 | B． | $\frac{1}{2}$ | C． | $\frac{{\sqrt{3}}}{2}$ | D． | $\sqrt{3}$ |
分析 首先求得∠FAD的度数，然后利用三角函数求得DF的长，然后利用三角形面积公式即可求解．
解答 
解：∵△ABC是等腰直角三角形，
∴∠CAB=45°，
又∵∠CAF=15°，
∴∠FAD=30°，
又∵在直角△ADF中，AF=AC=$\sqrt{3}$，
∴DF=AF•tan∠FAD=$\sqrt{3}$×$\frac{\sqrt{3}}{3}$=1，
∴S阴影=$\frac{1}{2}$AF•DF=$\frac{1}{2}$×$\sqrt{3}$×1=$\frac{\sqrt{3}}{2}$．
故选C．
点评 本题考查了图形的旋转以及三角函数，正确理解旋转角的定义，求得∠FAD的度数是关键．
练习册系列答案
相关题目
如图，一条街道的两个拐角∠ABC和∠BCD均为150°，街道AB与CD平行吗？为什么？
5．有一个角是30°的直角三角形，斜边为1cm，则斜边上的高为（ ）cm．
| A． | $\frac{1}{4}$ | B． | $\frac{1}{2}$ | C． | $\frac{\sqrt{3}}{4}$ | D． | $\frac{\sqrt{3}}{2}$ |
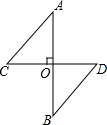如图，AB⊥CD于O，且AO=BO，根据提示，添加一个条件使得Rt△AOC≌Rt△BOD．
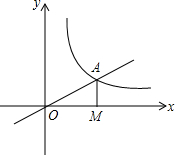如图，正比例函数y=$\frac{1}{2}$x的图象与反比例函数y=$\frac{k}{x}$（k≠0）在第一象限的图象交于A点，过A点作x轴的垂线，垂足为M，已知△OAM的面积为1．如果B为反比例函数在第一象限图象上的点（点B与点A不重合），且B点的横坐标为1，在x轴上求一点P，使PA+PB最小．
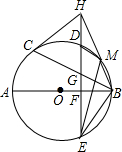如图，AB、BC分别是⊙O的直径和弦，点D为$\widehat{BC}$上一点，弦DE交⊙O于点E，交AB于点F，交BC于点G，过点C的切线交ED的延长线于H，且HC=HG，连接BH，交⊙O于点M，连接MD、ME、BE．求证：