题目内容
6.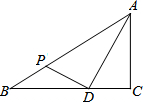 如图,△ABC中,∠C=90°,AD平分∠BAC,BD=4cm,CD=3cm,点P是边AB上的动点,则DP长的最小值为3cm.
如图,△ABC中,∠C=90°,AD平分∠BAC,BD=4cm,CD=3cm,点P是边AB上的动点,则DP长的最小值为3cm.
分析 先根据勾股定理求出CD的长,再过点D作DE⊥AB于点E,由垂线段最短可知当P与E重合时DP最短,根据角平分线的性质即可得出结论.
解答  解:过点D作DE⊥AB于点E,由垂线段最短可知当P与E重合时DP最短,
解:过点D作DE⊥AB于点E,由垂线段最短可知当P与E重合时DP最短,
∵AD平分∠CAB交BC于D,
∴DE=CD=3,即线段DP的最小值为3.
故答案为:3.
点评 本题考查的是角平分线的性质,熟知角的平分线上的点到角的两边的距离相等是解答此题的关键.

练习册系列答案
相关题目
4.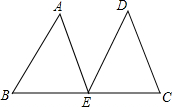 如图,E为BC的中点,AB=DE,∠B=∠DEC,则下列结论中不成立的是( )
如图,E为BC的中点,AB=DE,∠B=∠DEC,则下列结论中不成立的是( )
 如图,E为BC的中点,AB=DE,∠B=∠DEC,则下列结论中不成立的是( )
如图,E为BC的中点,AB=DE,∠B=∠DEC,则下列结论中不成立的是( )| A. | ∠B=∠C | B. | ∠A=∠D | C. | AE=CD | D. | AE∥CD |
16.实际测量一座山的高度时,可在若干个观测点中测量每两个相邻可视观测点的相对高度,然后用这些相对高度计算出山的高度.下表是某次测量数据的部分记录(用A-C表示观测点A相对观测点C的高度)根据这次测量的数据:
则可得观测点A相对观测点B的高度是230米.
| A-C | C-D | E-D | E-F | G-F | B-G |
| 90m | 80m | 50 | -40m | -70m | 20m |
 如图,一条街道的两个拐角∠ABC和∠BCD均为150°,街道AB与CD平行吗?为什么?
如图,一条街道的两个拐角∠ABC和∠BCD均为150°,街道AB与CD平行吗?为什么?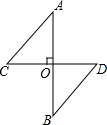 如图,AB⊥CD于O,且AO=BO,根据提示,添加一个条件使得Rt△AOC≌Rt△BOD.
如图,AB⊥CD于O,且AO=BO,根据提示,添加一个条件使得Rt△AOC≌Rt△BOD.