题目内容
14．（1）解方程组：$\left\{\begin{array}{l}{2x+y+z=-1}\\{3y-z=-1}\\{3x+2y+3z=-5}\end{array}\right.$．（2）若ax=10，ay=2，求a2x-y的值．
分析 （1）用加减消元法或代入法先把三元一次方程组化为二元一次方程组再求解．
（2）根据同底数幂的除法，可得要求的形式，根据幂的乘方，可得答案．
解答 解：（1）$\left\{\begin{array}{l}{2x+y+z=-1①}\\{3y-z=-1②}\\{3x+2y+3z=-5③}\end{array}\right.$
由②得z=3y+1④，
把z=3y+1分别代入①③得$\left\{\begin{array}{l}{2x+4y=-2}\\{3x+11y=-8}\end{array}\right.$
解得$\left\{\begin{array}{l}{x=1}\\{y=-1}\end{array}\right.$
把y=-1代入④得z=-2，
∴原方程组的解为$\left\{\begin{array}{l}{x=1}\\{y=-1}\\{z=-2}\end{array}\right.$．
（2）a2x-y=a2x÷ay
=（ax）2÷ay
=102÷2
=50．
点评 本题考查了解三元一次方程组，同底数幂的乘方以及同底数幂的除法；解三元一次方程组关键是先把三元一次方程组化为二元一次方程组，再用解二元一次方程组的知识求解．
练习册系列答案
寒假学与练系列答案
相关题目
4．在一个不透明的袋子中装有红、黄两种颜色的球共20个，每个球除颜色外完全相同．某学习兴趣小组做摸球实验，将球搅匀后从中随机摸出1个球，记下颜色后再放回袋中，不断重复．下表是活动进行中的部分统计数据．
（1）完成上表；
（2）“摸到红球”的概率的估计值是0.6（精确到0.1）
（3）试估算袋子中红球的个数．
| 摸球的次数n | 100 | 150 | 200 | 500 | 800 | 1000 |
| 摸到红球的次数m | 59 | 96 | 118 | 290 | 480 | 601 |
| 摸到红球的频率$\frac{m}{n}$ | 0.59 | 0.64 | 0.58 | 0.58 | 0.60 | 0.601 |
（2）“摸到红球”的概率的估计值是0.6（精确到0.1）
（3）试估算袋子中红球的个数．
如图，△ABC中，∠A=30°，∠B=62°，CE平分∠ACB，CD⊥AB于D，DF⊥CE于F，求∠CDF的度数．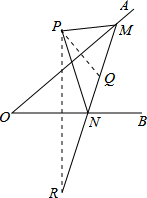
如图，点P是∠AOB外一点，点M、N分别是∠AOB两边上的点，点P关于OA的对称点Q恰好落在线段MN上，点P关于OB的对称点R落在线段MN的延长线上．若PM=2.5cm，PN=3cm，MN=4cm，则线段QR的长为4.5cm．
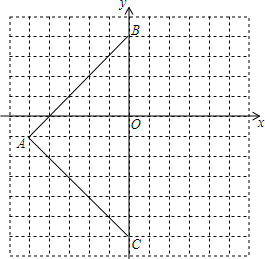如图，三角形ABC在平面直角坐标系中，三个顶点坐标分别为A（-5，-1）、B（0，4）、C（0，-6）．
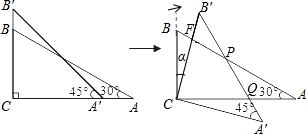如图所示，∠C=90°，Rt△ABC中，∠A=30°，Rt△A′B′C中，∠A=45°，点A′、B分别在线段AC、B′C上．将△A′B′C绕直角顶点C顺时针旋转一个锐角α时，边A′B′分别交AB、AC于P、Q，且△APQ为等腰三角形，则锐角α的度数15°．