题目内容
11.计算:(1)$\sqrt{8}+2\sqrt{7}-\sqrt{28}-\sqrt{2}$
(2)$\sqrt{\frac{7}{3}}÷\sqrt{2\frac{1}{3}×\sqrt{\frac{2}{3}}}$.
分析 (1)先把各二次根式化为最简二次根式,然后合并即可;
(2)根据二次根式的乘除法则运算.
解答 解:(1)原式=2$\sqrt{2}$+2$\sqrt{7}$-2$\sqrt{7}$-$\sqrt{2}$
=$\sqrt{2}$;
(2)原式=$\sqrt{\frac{7}{3}×\frac{3}{7}×\frac{2}{3}}$
=$\frac{\sqrt{6}}{3}$.
点评 本题考查了二次根式的计算:先把各二次根式化为最简二次根式,再进行二次根式的乘除运算,然后合并同类二次根式.在二次根式的混合运算中,如能结合题目特点,灵活运用二次根式的性质,选择恰当的解题途径,往往能事半功倍.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
2.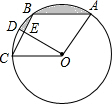 如图,在⊙O中有一个菱形ABCO,∠ABC=120°,OD⊥CB于点E,交⊙O于点D,若OE=2$\sqrt{3}$,则阴影部分的面积为( )
如图,在⊙O中有一个菱形ABCO,∠ABC=120°,OD⊥CB于点E,交⊙O于点D,若OE=2$\sqrt{3}$,则阴影部分的面积为( )
 如图,在⊙O中有一个菱形ABCO,∠ABC=120°,OD⊥CB于点E,交⊙O于点D,若OE=2$\sqrt{3}$,则阴影部分的面积为( )
如图,在⊙O中有一个菱形ABCO,∠ABC=120°,OD⊥CB于点E,交⊙O于点D,若OE=2$\sqrt{3}$,则阴影部分的面积为( )| A. | 4π-12$\sqrt{3}$ | B. | 4π-6$\sqrt{3}$ | C. | 4π | D. | 6π |
19.下列各式计算结果为a7的是( )
| A. | (-a)2•(-a)5 | B. | (-a)2•(-a5) | C. | (-a2)•(-a)5 | D. | (-a)•(-a)6 |
6.现有一只蜗牛和一只乌龟从同一点分别沿正东和正南方向爬行,蜗牛的速度为14厘米/分钟,乌龟的速度为48厘米/分钟,5分钟后,蜗牛和乌龟的直线距离为( )
| A. | 300厘米 | B. | 250厘米 | C. | 200厘米 | D. | 150厘米 |